搜索
【题目】为了调查某小区居民的用水情况，随机抽查了10户家庭的月用水量，结果如下表：
月用水量（吨） | 4 | 5 | 6 | 9 |
户数 | 3 | 4 | 2 | 1 |
则关于这10户家庭的月用水量，下列说法错误的是 （ ）
A.中位数是5吨
B.众数是5吨
C.极差是3吨
D.平均数是5．3吨
参考答案：
【答案】C
【解析】由统计表可知中位数是5，众数是5，故A、B正确，极差是9-4=5，故C错误，平均数是 
=5．3，故D正确；
所以答案是：C．
【考点精析】解答此题的关键在于理解算术平均数的相关知识，掌握总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数，以及对中位数、众数的理解，了解中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnn均为等腰直角三角形，且∠C1＝∠C2＝∠C3＝…＝∠n＝90°，点A1、A2、A3、…、An和点B1、B2、B3、…、Bn分别在正比例函数y＝
x和y＝﹣x的图象上，且点A1、A2、A3、…、An的横坐标分别为1，2，3…n，线段A1B1、A2B2、A3B3、…、AnBn均与y轴平行．按照图中所反映的规律，则△AnBnn的顶点n的坐标是_____；线段C2018C2019的长是_____．（其中n为正整数）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
x2+ x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6， 
）在抛物线上，直线AC与y轴交于点D．
（1）求c的值及直线AC的函数表达式；
（2）点P在x轴正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．
①求证：△APM∽△AON；
②设点M的横坐标为m，求AN的长（用含m的代数式表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点C是AB上一点，△ACM、△CBN都是等边三角形．
（1）说明AN＝MB；
（2）将△ACM绕点C按逆时针旋转180°，使A点落在CB上，请对照原题图画出符合要求的图形；
（3）在（2）所得到的图形中，结论“AN＝BM”是否成立？若成立，请说明理由；若不成立，也请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长是4，点E是BC的中点，连接DE，DF⊥DE交BA的延长线于点F．连接EF、AC，DE、EF分别与C交于点P、Q，则PQ＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以等边三角形ABC的BC边为直径画半圆，分别交AB，AC于点E，D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为（ ）
A.4
B.
C.6
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中,延长AB到点E,使BE＝AB,连接DE交BC于点F,则下列结论不一定成立的是（ ）
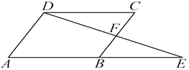
A. ∠E＝∠CDF B. BE＝CD C. ∠ADE＝∠BFE D. BE＝2CF
相关试题
