【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB,AC于点E,D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4
B.![]()
C.6
D.![]()
参考答案:
【答案】B
【解析】连接OD, 
∵DF是切线,∴∠ODF=90°,
∵∠C=60°,OD=OC= ![]() BC,
BC,
∴△OCD是等边三角形,
∴CD=OC= ![]() BC=
BC= ![]() AC,
AC,
∴OD//AB,∴∠AFD=∠ODF=90°,
∵∠A=60°,
∴∠ADF=30°,
∴AD=2AF=4,
∴AC=8,
∴AB=AC=8,
∵AF=2,
∴BF=6,
∵∠FBG=90°,∠B=60°,
∴FG=FB·sin60°=3 ![]() ;
;
所以答案是:B.
【考点精析】掌握含30度角的直角三角形和切线的性质定理是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:
月用水量(吨)
4
5
6
9
户数
3
4
2
1
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A.中位数是5吨
B.众数是5吨
C.极差是3吨
D.平均数是5.3吨 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
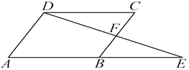
A. ∠E=∠CDF B. BE=CD C. ∠ADE=∠BFE D. BE=2CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户
张大爷
王阿姨
小明家
月用水量/m3
6
15
17
月应缴纳水费/元
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
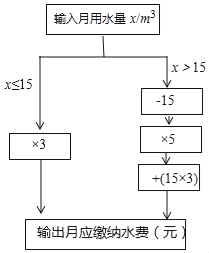
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 .
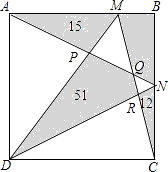
相关试题

