【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨![]() ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
参考答案:
【答案】(1)该酒店豪华间有50间,旺季每间价格为800元(2)当![]() 时,
时,![]()
【解析】
试题分析:(1)∵旺季每间比淡季上涨![]() ,∴旺季每间是淡季1
,∴旺季每间是淡季1![]() ,根据此等量关系列分式方程解应用题
,根据此等量关系列分式方程解应用题
(2)设上涨m元,利润为![]() 。价格每增加25元,每天入住房间数减少1间,∴入住房间数
。价格每增加25元,每天入住房间数减少1间,∴入住房间数![]() ,得利润表达式
,得利润表达式![]() =
=![]() ,再求最值.
,再求最值.
试题解析: (1)设有![]() 间豪华间,由题可得
间豪华间,由题可得
![]()
解得![]() ,经检验
,经检验![]() 是原方程的根
是原方程的根
则:![]()
答:该酒店豪华间有50间,旺季每间价格为800元。
(2)设上涨m元,利润为![]() ,则
,则![]()
因为![]() ,所以抛物线开口向下
,所以抛物线开口向下
所以当![]() 时,
时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、
 ,二次函数
,二次函数 的图象经过点A、B,且a、m满足
的图象经过点A、B,且a、m满足 为常数
为常数 .
. 若一次函数
若一次函数 的图象经过A、B两点.
的图象经过A、B两点. 当
当 、
、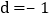 时,求k的值;
时,求k的值; 若y随x的增大而减小,求d的取值范围;
若y随x的增大而减小,求d的取值范围; 当
当 且
且 、
、 时,判断直线AB与x轴的位置关系,并说明理由;
时,判断直线AB与x轴的位置关系,并说明理由; 点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,则折痕AE的长为( )

A.
 cmB.
cmB. cmC.12cmD.13 cm
cmC.12cmD.13 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数
 的图象于点B,
的图象于点B, .
. 求反比例函数的解析式;
求反比例函数的解析式; 若
若 、
、 是该反比例函数图象上的两点,且
是该反比例函数图象上的两点,且 时,
时, ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列三个结论:① EF=BE+CF;②∠BGC=90°+
 ∠A;③点G到△ABC各边的距离相等;其中正确的结论有_________(填序号)
∠A;③点G到△ABC各边的距离相等;其中正确的结论有_________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、图②、图③是3×3的正方形网格,每个网格图中有3个小正方形己涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)在图①中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)在图②中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)在图③中选取2个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形.(请将三个小题依次作答在图①、图②、图③中,均只需画出符合条件的一种情形)

相关试题

