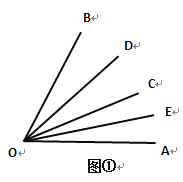
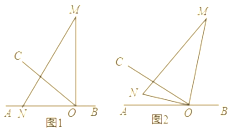
【题目】如图①,(1)∠AOB=60°,∠BOC=36°OD平分∠BOC,OE平分∠AOC,则∠EOD=____度;
(2)若∠AOB=90°,OD平分∠BOC,OE平分∠AOC,则∠EOD=__________;
(3)若∠AOB=α,其它条件同(2),则∠EOD=_________________.
类比应用:
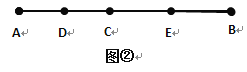
如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
参考答案:
【答案】(1)30;(2)45度;(3)![]() α;类比应用:DE=
α;类比应用:DE=![]() AB,见解析.
AB,见解析.
【解析】
(1)根据角平分线的定义,∠COD=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,所以∠EOD=
∠AOC,所以∠EOD=![]() ∠AOB,代入数据计算即可;
∠AOB,代入数据计算即可;
(2)与(1)的求解与解答思路相同;
(3)与(1)的求解与解答思路相同;
类比应用:把题中的∠AOB换成线段AB,相应的角平分线换成中点即可.
解:(1)∵∠AOB=60°,∠BOC=36°
∴∠AOC=24°
∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=18°,∠COE=
∠BOC=18°,∠COE=![]() ∠AOC=12°,
∠AOC=12°,
∴∠EOD=∠DOC+∠COE=![]() ∠BOC+
∠BOC+![]() ∠AOC=
∠AOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,
∠AOB,
∵∠AOB=60°,
∴∠EOD=![]() ×60°=30°;
×60°=30°;
(2)同理∠EOD=![]() ∠AOB=
∠AOB=![]() ×90°=45°;
×90°=45°;
(3)同理∠EOD=![]() ∠AOB=
∠AOB=![]() ;
;
类比应用:如图②,∵D是AC的中点,E是BC的中点,
∴DC=![]() AC,EC=
AC,EC=![]() BC;
BC;
∴DE=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() AB.
AB.
故答案为:(1)30;(2)45度;(3)![]() α;类比应用:DE=
α;类比应用:DE=![]() AB,见解析.
AB,见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
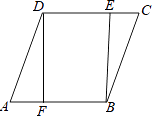
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π).

-
科目: 来源: 题型:
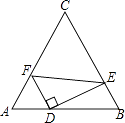
查看答案和解析>>【题目】如图.在等边△ABC中,AC=8,点D,E,F分别在三边AB,BC,AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板 (∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方,将如图中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周。
(1)几秒后ON与OC重合?
(2)如图,经过t秒后,MN∥AB,求此时t的值。
(3)若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC与OM重合?请画图并说明理由。
(4)在(3)的条件下,求经过多长时间OC平分∠MOB?请画图并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
相关试题

