搜索
【题目】如图，在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？
参考答案：
【答案】解：AC=120×=12(nmile)，BC=50×=5(nmile)，又因为AB=13nmile，所以AC2+BC2=AB2 ， 所以△ABC是直角三角形，可知∠CAB+∠CBA=90°，由∠CBA=50°，知∠CAB=40°，所以甲巡逻艇的航向为北偏东50°
【解析】运用勾股定理的逆定理可判断△ABC是直角三角形，再根据直角三角形两锐角互余可求甲巡逻艇的航向。
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a,b,c是直角三角形的三条边长，斜边c上的高的长是h，给出下列结论：
①以a2 ， b2 ， c2的长为边的三条线段能组成一个三角形；②以
，
，
的长为边的三条线段能组成一个三角形；③以a+b，c+h，h的长为边的三条线段能组成直角三角形；④以
,
,
的长为边的三条线段能组成直角三角形，正确结论的序号为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c为正数，满足如下两个条件：
a+b+c=32 ①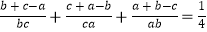
②
是否存在以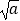
， 
， 
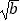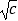为三边长的三角形？如果存在，求出三角形的最大内角． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列事件中，最适合采用普查的是( )
A.了解一批灯泡的使用寿命B.了解中央电视台《最强大脑》栏目的收视率
C.了解全国中学生体重情况D.了解某班学生对“七步洗手法”的知晓率
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P（﹣1，2）关于y轴对称点的坐标是（ ）
A. （1，2） B. （﹣1，﹣2） C. （1，﹣2） D. （2，﹣1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题
（1）如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若PA2+PB2=PC2，证明∠PQC=90°；
（2）如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形一边长是6，另一边长是12，则周长是（ ）
A. 24 B. 30 C. 24或30 D. 18
相关试题
