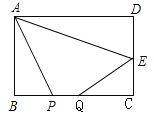
【题目】如图,在矩形ABCD中 ,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为( )
A. 1 B. 2 C. 2![]() D. 4
D. 4
参考答案:
【答案】D
【解析】要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.
如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵GH=DF=6,EH=2+4=6,∠H=90°,
∴∠GEH=45°.
设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,
在△CQE中,
∵∠QCE=90°,∠CEQ=45°,
∴CQ=EC,
∴6-x=2,
解得x=4.
故选D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
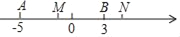
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=
 ,则CF的长为_______
,则CF的长为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,P为边AB上一点.

(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
相关试题

