【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,AB,BC,点E从点A出发,以每秒 ![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.
参考答案:
【答案】
(1)解:将B(4,4)和C(6,0)代入抛物线y=ax2+bx+4得:
![]() ,
,
解得: 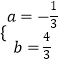 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
(2)解:如图1,由题意得:AE= ![]() t,
t, 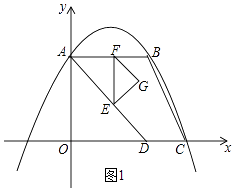
∵A(0,4),B(4,4),
∴AB⊥y轴,且AB∥x轴,
∵OA=OD=4,
∴△AOD是等腰直角三角形,
∴∠ADO=∠BAD=45°,
∴△AFE是等腰直角三角形,
∴AF=EF=t,
∵△EFG是等腰直角三角形,
∴G(t+ ![]() t,4﹣
t,4﹣ ![]() t),
t),
即:点G( ![]() ,4﹣
,4﹣ ![]() t),
t),
将点G( ![]() ,4﹣
,4﹣ ![]() t)代入到抛物线得:
t)代入到抛物线得:
4﹣ ![]() t=﹣
t=﹣ ![]() (
( ![]() )2+
)2+ ![]() +4,
+4,
解得:t1=0(舍),t2= ![]() ,
,
答:当t= ![]() 时,点G落在抛物线上
时,点G落在抛物线上
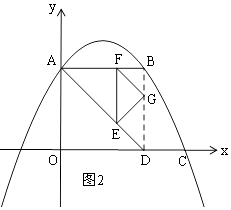
(3)解:如图2,连接BD,当G在BD上时,
![]() =4,
=4,
t= ![]() ,
,
①当0≤t≤ ![]() 时,如图3,
时,如图3, 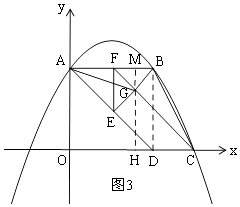
过G作GH⊥x轴于H,延长HG交AB于M,则GM⊥AB,
∵B(4,4),D(4,0),
∴BD⊥x轴,
∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC,
4= ![]() (4﹣
(4﹣ ![]() +4)(4﹣
+4)(4﹣ ![]() )+
)+ ![]() ×4×(6﹣4)﹣
×4×(6﹣4)﹣ ![]() (6﹣
(6﹣ ![]() )(4﹣
)(4﹣ ![]() t),
t),
4= ![]() t,
t,
解得:t= ![]() ,
,
∴AM= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
GM= ![]() t=
t= ![]() ×
× ![]() =
= ![]() ,
,
在Rt△AGM中,由勾股定理得:AG= ![]() =
= ![]() =
= ![]() ;
;
∴当t= ![]() 时,此时点G运动的路径长为
时,此时点G运动的路径长为 ![]() ;
;
②当G在BC上时,如图4, 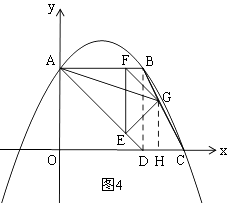
tan∠C= ![]() =2,
=2,
∴GH=2HC,
∴4﹣ ![]() t=2(6﹣
t=2(6﹣ ![]() ),
),
t= ![]() ,
,
当 ![]() <t≤
<t≤ ![]() 时,如图5,
时,如图5, 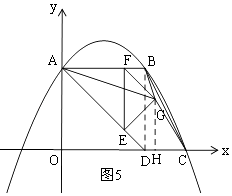
S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC,
4= ![]() ×4×2﹣
×4×2﹣ ![]() (4﹣
(4﹣ ![]() +4)(
+4)( ![]() t﹣4)﹣
t﹣4)﹣ ![]() ×
× ![]() ,
,
t= ![]() (不在此范围内,不符合题意),
(不在此范围内,不符合题意),
③当E与D重合时,F与B重合,如图6, 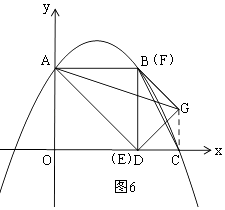
t= ![]() =4,
=4,
∴G(6,2),
∴AG= ![]() =2
=2 ![]() ,
,
∴S△BCG=S梯形BDCG﹣S△BDC= ![]() ×2×(4+2)﹣
×2×(4+2)﹣ ![]() ×2×4=2,
×2×4=2,
∴当t>4时,如图7, 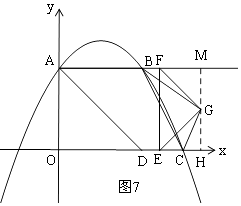
由题意得:DE=t﹣4,
∴OE=t﹣4+4=t,
∴OH=OE+EH=t+2,
EH=2,GM=GH=2,
BM=t+2﹣4=t﹣2,
CH=t+2﹣6=t﹣4,
过G作MH⊥x轴,交x轴于H,交直线AB于M,
∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH,
4= ![]() (t﹣4+t﹣2)×4﹣
(t﹣4+t﹣2)×4﹣ ![]() ×2×(t﹣2)﹣
×2×(t﹣2)﹣ ![]() ×2×(t﹣4),
×2×(t﹣4),
t=5,
当t=5时,点G的运动路径分为两部分组成:
i)点G从A运动到D时,运动路径为:如图6中的AG长,即为2 ![]() ;
;
ii)点G从D点继续在射线DC上运动1秒时,路径为1;
所以当t=5时,此时点G运动的路径长度为1+2 ![]() .
.
综上所述:当t1= ![]() 秒,此时路径长度为
秒,此时路径长度为 ![]() ,
,
当t2=5秒,此时路径长度为1+2 ![]() .
.
【解析】(1)利用待定系数法把B、C坐标代入解析式即可;(2)用t 的代数式表示出G的横纵坐标,代入抛物线解析式即可;(3)t=![]() 时,E到D,因此时间t 分为当①0≤t≤
时,E到D,因此时间t 分为当①0≤t≤ ![]() , ②
, ② ![]() <t
<t![]()
![]() ③t=4 4)t>4;5).t=5时,点G的运动路径分为两部分组成,综合起来t=
③t=4 4)t>4;5).t=5时,点G的运动路径分为两部分组成,综合起来t=![]() 或t=5,分别求出对应的路径长.
或t=5,分别求出对应的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两家加工厂都想加工这批产品,已知红星厂单独加工比巨星厂单独加工这批产品多用20天,红星厂每天可加工16件产品,巨星厂每天可加工24件产品,公司需付给红星厂每天加工费800元,付给巨星厂每天加工费1200元.
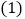 这个公司要加工多少件新产品?
这个公司要加工多少件新产品?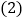 公司的产品可由一家工厂单独加工完成,也可由两家工厂合作完成,在加工过程中公司需另派一名工程师每天到厂家进行指导,并支付工程师每天10元的午餐补助,请你帮助公司从所有可供选择的方案中,选择一种既省钱又省时的加工方案.
公司的产品可由一家工厂单独加工完成,也可由两家工厂合作完成,在加工过程中公司需另派一名工程师每天到厂家进行指导,并支付工程师每天10元的午餐补助,请你帮助公司从所有可供选择的方案中,选择一种既省钱又省时的加工方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一架梯子AB斜靠在墙面上,且AB的长为25米.
(1)若梯子底端离墙角的距离OB为7米,求这个梯子的顶端A距地面有多高?
(2)在(1)的条件下,如果梯子的顶端A下滑4米到点A,,那么梯子的底端B在水平方向滑动的距离BB,为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

-
科目: 来源: 题型:
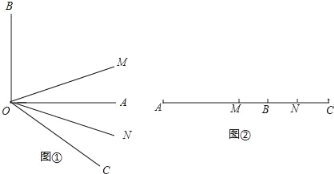
查看答案和解析>>【题目】如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,∠AOC=β.(α,β为锐角),其它条件不变,求出∠MON的度数;
(3)其实线段的计算与角的计算存在着紧密的联系,如图②线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,求MN的长(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题.
例题:若m2+2mn+2n26n+9=0,求m和n的值.
解:∵m2+2mn+2n26n+9=0即:
∴m2+2mn+n2+n26n+9=0
∴

∴即:m+n=0,n-3=0
∴m=3,n=3
(1)若
 ,求
,求 的值.
的值.(2)若三角形三边a,b,C都是正整数,且满足
 ,判断三角形的形状.
,判断三角形的形状.
相关试题

