【题目】如图所示,一架梯子AB斜靠在墙面上,且AB的长为25米.
(1)若梯子底端离墙角的距离OB为7米,求这个梯子的顶端A距地面有多高?
(2)在(1)的条件下,如果梯子的顶端A下滑4米到点A,,那么梯子的底端B在水平方向滑动的距离BB,为多少米?

参考答案:
【答案】(1)24米;(2)8米
【解析】试题分析:(1)在Rt△AOB中,根据勾股定理可以计算出AO,(2)先根据题意顶端A下滑4米到点A’,可计算出A’O,在Rt△A’OB’中,根据勾股定理可以计算出OB’,然后根据线段和差关系计算出BB’.
试题解析:(1) 在Rt△AOB中,根据勾股定理可得: AO=![]() 米,
米,
答: 顶端A距地面有24米.
(2) 在Rt△A’OB’中, A’O=24-4=20, 根据勾股定理可得:
OB’=![]() ,
,
所以BB’=15-7=8米,
答: 梯子的底端B在水平方向滑动的距离BB’为8米.
点睛:本题主要考查利用勾股定理解决实际问题,解决本题的关键是熟练利用勾股定理进行计算.
-
科目: 来源: 题型:
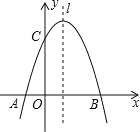
查看答案和解析>>【题目】如图,已知抛物线y=
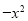 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=
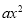 +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=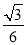 ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥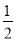 .正确的是( ).
.正确的是( ).A.①② B.③④ C.①②③ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020的绝对值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=b+3,则2a-2b+1的值为( )
A. 7 B. 6 C. 5 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为∠MON平分线上一点,且OP=
 ,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=
,PA⊥ON,垂足为A,B为射线OM上一动点,若AP=1,PB=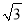 ,则OB=______.
,则OB=______.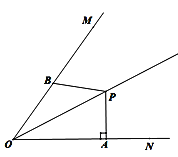
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中正确的是( )
A.x3x2=2x6
B.(﹣3x3)2=﹣6x6
C.(x3)2=x5
D.x6÷x2=x4
相关试题

