【题目】已知,正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线![]() ,分别交AB、CD于点M、N.
,分别交AB、CD于点M、N.
(1)如图,求证:![]() ;
;
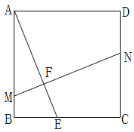
(2)如图,当点F为AE中点时,连接正方形的对角线BD,MN与BD交于点G,连接BF,求证:![]() ;
;
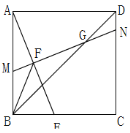
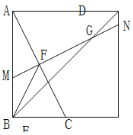
(3)如图,在(2)的条件下,若![]() ,
,![]() ,求BM的长度.
,求BM的长度.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由正方形的性质得出∠B=90°,得出∠BAE+∠AEB=90°,由垂直的性质得出∠BAE+∠AMN=90°,即可得出结论;
(2)连接AG、EG、CG,证明△ABG≌△CBG得出AG=CG,∠GAB=∠GCB,证出EG=CG,由等腰三角形的性质得出∠GEC=∠GCE,证出∠AGE=90°,由直角三角形斜边上的中线性质得出BF=![]() AE,FG=
AE,FG=![]() AE,即可得出结论;
AE,即可得出结论;
(3)过G作![]() 交AD于点P,交BC于点Q,证明DP=PG=2,连接ME,证明MN是AE的垂直平分线,得
交AD于点P,交BC于点Q,证明DP=PG=2,连接ME,证明MN是AE的垂直平分线,得![]() ,
,![]() ,再证明
,再证明![]() 得
得![]() ,得
,得![]() ,进而得
,进而得![]() ,
,![]() 中,由勾股定理得
中,由勾股定理得![]() ,代入相关数据,从而得出结论.
,代入相关数据,从而得出结论.
(1)(1)证明:∵四边形ABCD是正方形,
∴∠B=90°,
∴∠BAE+∠AEB=90°,
∵MN⊥AE于F,
∴∠BAE+∠AMN=90°,
∴∠AEB=∠AMN;
(2)证明:连接AG、EG、CG,
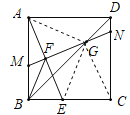
∵四边形ABCD是正方形,
∴AB=BC,∠ABG=∠CBG=45°,∠ABE=90°,
在△ABG和△CBG中,
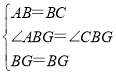 ,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠GAB=∠GCB,
∵MN⊥AE于F,F为AE中点,
∴AG=EG,
∴EG=CG,
∴∠GEC=∠GCE,
∴∠GAB=∠GEC,
∵∠GEB+∠GEC=180°,
∴∠GEB+∠GAB=180°,
∵四边形ABEG的内角和为360°,∠ABE=90°,
∴∠AGE=90°,
在Rt△ABE和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=![]() AE,FG=
AE,FG=![]() AE,
AE,
∴BF=FG;
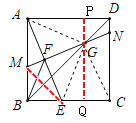
(3)过G作![]() 交AD于点P,交BC于点Q,则
交AD于点P,交BC于点Q,则![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() 即
即![]()
连接ME ∵![]() 于F,F为AE的中点,
于F,F为AE的中点,
∴MN是AE的垂直平分线
∴![]() ,
,![]()
由(2)知![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]()
∴![]()
∴![]()
∵![]()
∴四边形PDCQ为矩形
∴![]()
设![]()
∵E是BC中点
∴![]()
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
设![]()
∴![]()
![]() 中,由勾股定理得
中,由勾股定理得![]()
∴![]() 解得
解得![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
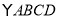 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作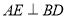 ,
,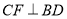 ,E、F为垂足.
,E、F为垂足.(1)如图,求证:
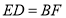 ;
;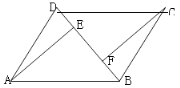
(2)如图,连接AC,设AC、BD交于点O,若
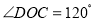 .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.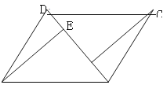
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A,B两点(点A在点B的左侧),抛物线的顶点为C,直线y=x+3与x轴交于点D.
(Ⅰ)求抛物线的顶点C的坐标及A,B两点的坐标;
(Ⅱ)将抛物线y=x2﹣6x+9向上平移1个单位长度,再向左平移t(t>0)个单位长度得到新抛物线,若新抛物线的顶点E在△DAC内,求t的取值范围;
(Ⅲ)点P(m,n)(﹣3<m<1)是抛物线y=x2﹣6x+9上一点,当△PAB的面积是△ABC面积的2倍时,求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地2016年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1600万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前800户(含第800户)每户每天奖励10元,800户以后每户每天奖励5元,按租房400天计算,求2018年该地至少有多少户享受到优先搬迁租房奖励.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O是直线AB上一点,射线OD,OE分别是∠BOC,∠AOC的平分线.

(1)图中共有几对互余角?请写出来
(2)若∠AOE=31°,求∠AOC和∠DOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽取6名同学参加体能测试,成绩如下:75,95,85,80,90,85. 下列表述不正确的是 ( ) .
A. 众数是 85 B. 中位数是85 C. 平均数是85 D. 方差是15
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点
 出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:(1)小虫离开出发点
 最远是多少厘米?
最远是多少厘米?(2)小虫最后是否回到原点
 ?
?(3)在爬行过程中看,如果每爬行1cm奖励2粒芝麻,则小虫共可得到多少粒芝麻?
相关试题

