【题目】小虫从某点![]() 出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-10.问:
(1)小虫离开出发点![]() 最远是多少厘米?
最远是多少厘米?
(2)小虫最后是否回到原点![]() ?
?
(3)在爬行过程中看,如果每爬行1cm奖励2粒芝麻,则小虫共可得到多少粒芝麻?
参考答案:
【答案】(1)12cm;(2)小虫最后回到原点![]() ;(3)小虫可得到108粒芝麻.
;(3)小虫可得到108粒芝麻.
【解析】
(1)通过计算小虫每次爬完之后离原点的距离即可得出答案;
(2)利用有理数的加法进行计算然后看最后的结果是否为0,若为0,则回到原点,反之则没有;
(3)将每个数的绝对值相加,然后再乘2即可得出答案.
(1)根据题意可知,
小虫第一次爬完之后离原点的距离为5cm
小虫第二次爬完之后离原点的距离为![]()
小虫第三次爬完之后离原点的距离为![]()
小虫第四次爬完之后离原点的距离为![]()
小虫第五次爬完之后离原点的距离为![]()
小虫第六次爬完之后离原点的距离为![]()
小虫第七次爬完之后离原点的距离为![]()
∴小虫离开出发点![]() 最远是12cm.
最远是12cm.
(2)∵![]()
∴小虫最后回到原点![]() .
.
(3)![]() ,
,
![]() (粒)
(粒)
∴小虫可得到108粒芝麻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线
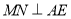 ,分别交AB、CD于点M、N.
,分别交AB、CD于点M、N.(1)如图,求证:
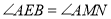 ;
;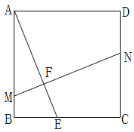
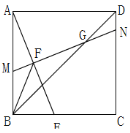
(2)如图,当点F为AE中点时,连接正方形的对角线BD,MN与BD交于点G,连接BF,求证:
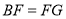 ;
;
(3)如图,在(2)的条件下,若
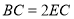 ,
,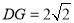 ,求BM的长度.
,求BM的长度.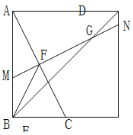
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O是直线AB上一点,射线OD,OE分别是∠BOC,∠AOC的平分线.

(1)图中共有几对互余角?请写出来
(2)若∠AOE=31°,求∠AOC和∠DOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽取6名同学参加体能测试,成绩如下:75,95,85,80,90,85. 下列表述不正确的是 ( ) .
A. 众数是 85 B. 中位数是85 C. 平均数是85 D. 方差是15
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(
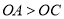 )的长是方程
)的长是方程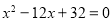 的两个根.
的两个根.(1)如图,求点A的坐标;
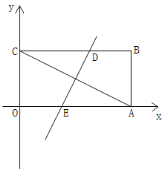
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有
 等著名景点,该市旅游部门统计绘制出今年“五·一”长假期间旅游情况统计图,根据以下信息解答下列问题:
等著名景点,该市旅游部门统计绘制出今年“五·一”长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)今年“五·一”期间,该市周边景点共接待游客多少人?扇形统计图中
 景点所对应的圆心角的度数是多少?并补全条形统计图.
景点所对应的圆心角的度数是多少?并补全条形统计图.(2)根据近几年到该市旅游人数增长趋势,预计明年“五·一”节将有80万游客选择该市旅游,请估计有多少万人会选择去
 景点旅游?
景点旅游? -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程
 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
相关试题

