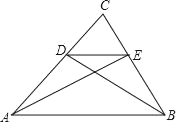
【题目】如图,点D、E分别在△ABC的边AC和BC上,∠C=90°,DE∥AB,且3DE=2AB,AE=13,BD=9,那么AB的长为_____.
参考答案:
【答案】![]()
【解析】分析:先设DE=2x,CD=2y,CE=2z,由于DE∥AB,3DE=2AB,根据平行线分线段成比例定理,可得AB=3x,AC=3y,BC=3z,而∠C=90°,利用勾股定理,可得y2+z2=x2①,(3y)2+(2z)2=132②,(2y)2+(3z)2=92③,解关于①②③的方程,可求x,从而可求AB.
详解:设DE=2x,CD=2y,CE=2z,
∵DE∥AB,3DE=2AB,
∴AB=3x,AC=3y,BC=3z,
又∵∠C=90°,
∴(2y)2+(2z)2=(2x)2,
即y2+z2=x2,①
同理(3y)2+(2z)2=132,②
(2y)2+(3z)2=92,③
②-①×4,得
5y2=169-4x2,④
①×9-③,得
5y2=9x2-81,⑤
⑤-④,得
x2=![]() ,
,
x=![]()
∴AB=3x=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】7张如图1的长为
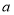 ,宽为b
,宽为b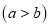 的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.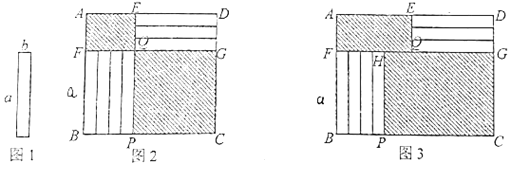
(1)如图2,点E、Q、P在同一直线上,点F、Q、G在同一直线上,右下角与左上角的阴影部分的面积的差为____________(用含
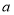 、
、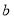 的代数式表示),矩形ABCD的面积为____________(用含
的代数式表示),矩形ABCD的面积为____________(用含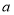 、
、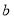 的代数式表示);
的代数式表示);(2)如图3,点F、H、Q、G在同一直线上,设右下角与左上角的阴影部分的面积的差为S,
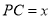 .
.①用
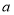 、
、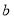 、
、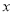 的代数式表示AE;
的代数式表示AE;②当BC的长度变化时,按照同样的放置方式,S始终保持不变,那么
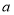 、
、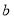 必须满足什么条件?
必须满足什么条件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B<90,BC>AB.作AE⊥BC于点E,AF⊥CD于点F,记∠EAF的度数为α,AE=a,AF=b.则以下选项错误的是( )

A. ∠D的度数为α
B. a∶b=CD∶BC
C. 若α=60,则平行四边形ABCD的周长为

D. 若α=60,则四边形AECF的面积为平行四边形ABCD面积的一半
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
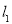 的解析式为
的解析式为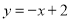 ,
,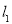 与
与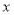 轴交于点
轴交于点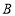 ,直线
,直线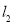 经过点
经过点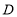 (0,5),与直线
(0,5),与直线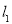 交于点
交于点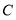 (﹣1,
(﹣1, ),且与
),且与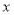 轴交于点
轴交于点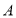 .
. (1)求点
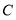 的坐标及直线
的坐标及直线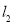 的解析式;
的解析式;(2)求△
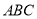 的面积.
的面积.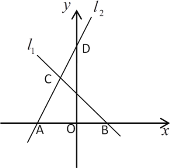
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,G是AD 上的任一点.计S1=S△BEF , S2=S△GFC ,S=S□ABCD ,则S=________S2=________S1 .
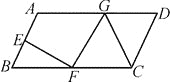
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某校在慈善爱心捐款活动中的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查.
(1)在抽取的样本中,捐款金额的平均数、中位数、众数各是多少?
(2)若该校九年级共有200人捐款,请你估计全校捐款的总金额约为多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,则∠FEB的度数是 .
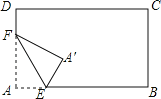
相关试题

