【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+
x+![]() 与y=x相交于点A,与x轴交于点B.
与y=x相交于点A,与x轴交于点B.
(1)填空:A的坐标是_______,B的坐标是___________;
(2)直线y=﹣![]() x+
x+![]() 上有点P(m,n),且点P在第四象限,设△AOP的面积为S,请求出S与m的函数关系式;
上有点P(m,n),且点P在第四象限,设△AOP的面积为S,请求出S与m的函数关系式;
(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.
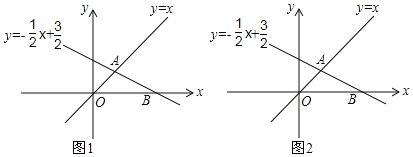
参考答案:
【答案】(1)A(1,1),B(3,0);(2)S=![]() ;(3)存在,D(﹣
;(3)存在,D(﹣![]() ,﹣
,﹣![]() ),D(
),D(![]() ,
,![]() ),D(3,3)或D(
),D(3,3)或D(![]() ,
,![]() ).
).
【解析】
(1)把直线y=-![]() x+
x+![]() 与y=x联立得出方程组求解即可得出点A的坐标,由直线y=-
与y=x联立得出方程组求解即可得出点A的坐标,由直线y=-![]() x+
x+![]() 与x轴交于点B,令y=0,求出x的值,即可得出B的坐标;
与x轴交于点B,令y=0,求出x的值,即可得出B的坐标;
(2)根据S = S△AOB+ S△POB即可解答;
(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,分四种情况①当OB=OD时,②当OD=OB时,③当OB=DB时,④当DO=DB时分别求解即可.
解:(1)∵直线y=﹣![]() x+
x+![]() 与y=x相交于点A,
与y=x相交于点A,
∴联立得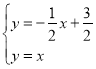 ,解得
,解得![]() ,
,
∴点A(1,1),
∵直线y=﹣![]() x+
x+![]() 与x轴交于点B,
与x轴交于点B,
∴令y=0,得﹣![]() x+
x+![]() =0,解得x=3,
=0,解得x=3,
∴B(3,0).
(2)S=S△AOB+S△OBP=![]()
![]()
(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,
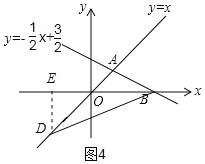
①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E
∵OB=3,点D在OA上,∠DOE=45°
∴DE=OE=![]() ,
,
∴D(﹣![]() ,﹣
,﹣![]() ),
),
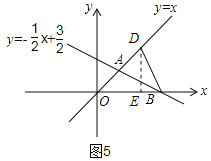
②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E
∵OB=3,点D在OA上,∠DOE=45°
∴DE=OE=![]() ,
,
∴D(![]() ,
,![]() ),
),
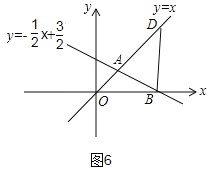
③如图6,当OB=DB时,
∵∠AOB=∠ODB=45°,
∴DB⊥OB,
∵OB=3,
∴D(3,3),
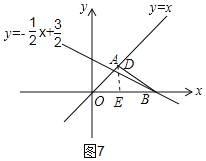
④如图7,当DO=DB时,作DE⊥x轴,交x轴于点E
∵∠AOB=∠OBD=45°,
∴OD⊥DB,
∵OB=3,
∴OE=![]() ,AE=
,AE=![]() ,
,
∴D(![]() ,
,![]() ).
).
综上所述,在直线OA上,存在点D(﹣![]() ,﹣
,﹣![]() ),D(
),D(![]() ,
,![]() ),D(3,3)或D(
),D(3,3)或D(![]() ,
,![]() ),使得△DOB是等腰三角形.
),使得△DOB是等腰三角形.
-
科目: 来源: 题型:
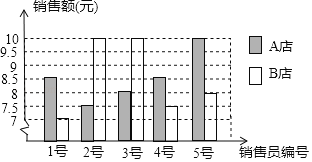
查看答案和解析>>【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数
中位数
众数
A店
8.5
B店
8
10
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是
是 的中点,点
的中点,点 是线段
是线段 的延长线上的一动点,连接
的延长线上的一动点,连接 ,过点
,过点 作
作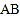 的平行线
的平行线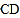 ,与线段
,与线段 的延长线交于点
的延长线交于点 ,连接
,连接 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形.
是平行四边形. 若
若 ,
, ,则在点
,则在点 的运动过程中:
的运动过程中:①当
 ________时,四边形
________时,四边形 是矩形,试说明理由;
是矩形,试说明理由;②当
 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当
 时,求
时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2分)矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是()
A. 16 B. 22或16 C. 26 D. 22或26
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是李刚同学在一次测验中解答的数学题:
①若
 ,则
,则 ,
,②方程
 的解为
的解为 ,
,③若
 两根的倒数和等于
两根的倒数和等于 ,则
,则 ,
,④若
 是方程
是方程 的解,则
的解,则 或
或 .
.其中答对的是________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
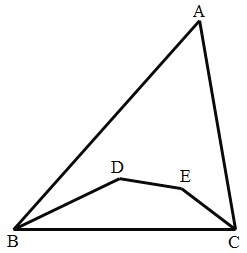
A.65°B.60°C.55°D.50°
相关试题

