【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:![]() ,长方形ABCO在坐标系中(如图1),点O为坐标系的原点.
,长方形ABCO在坐标系中(如图1),点O为坐标系的原点.
(1)求点B的坐标.
(2)如图2,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图3,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由

参考答案:
【答案】(1)B(-6,-3);(2)四边形MBNO的面积与t无关,在运动过程中面积不变,为定值9;(3)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据题意可得a=-6,c=-3,则可求A点,C点,B点坐标;
(2)设M、N同时出发的时间为t,则S四边形MBNO=S长方形OABC-S△ABM-S△BCN=18-![]() ×2t×3-
×2t×3-![]() ×6×(3-t)=9.与时间无关.即面积是定值,其值为9;
×6×(3-t)=9.与时间无关.即面积是定值,其值为9;
(3)根据三角形内角和定理和三角形外角等于不相邻的两个内角的和,可求∠CFE与∠D的数量关系.
解:解:(1)∵![]() 0,
0,
∴a=-6,c=-3
∴A(-6,0),C(0,-3)
∵四边形OABC是长方形
∴AO∥BC,AB∥OC,AB=OC=3,AO=BC=6
∴B(-6,-3);
(2)四边形MBNO的面积不变.
设M、N同时出发的时间为t,
S四边形MBNO=S长方形OABC-S△ABM-S△BCN=18-![]() ×2t×3-
×2t×3-![]() ×6×(3-t)=9,与时间无关.即面积是定值,其值为9;
×6×(3-t)=9,与时间无关.即面积是定值,其值为9;
(3)∠CFE=2∠D.
理由如下:如图,

∵∠CBE=∠CEB,
∴∠ECB=180°-2∠BEC,
∵CD平分∠ECF,
∴∠DCE=∠DCF,
∵AF∥BC,
∴∠CFE=180°-∠DCF-∠DCE-∠BCE=180°-2∠DCE-(180°-2∠BEC),
∴∠CFE=2∠BEC-2∠DCE,
∵∠BEC=∠D+∠DCE,
∴∠CFE=2(∠D+∠DCE)-2∠DCE,
∴∠CFE=2∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,E、F、M分别为AB、BC、CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成长方形的周长与面积的数值相等,则这个点叫做和谐点.
(1)判断点M
 是否为和谐点,并说明理由;
是否为和谐点,并说明理由;(2)若和谐点
 满足
满足 (
( 为常数),求点
为常数),求点 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中,对角线AC、BD交于O点,CE⊥BD于E,OF⊥AB 于F,BE:DE=1:3,OF=2cm,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,四个内角平分线相交于E、F, 若AB= 8cm,Ad=20cm,求EF的长度.
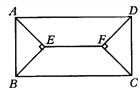
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是七年级二班参加社团活动人数的扇形统计图(每位同学只参加其中一个社团).根据统计图提供的信息,下列结论正确的是( )
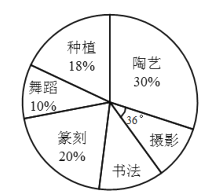
A. 参加摄影社的人数占总人数的
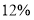
B. 参加篆刻社的扇形的圆心角度数是
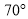
C. 参加种植社的同学比参加舞蹈社的多
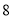 人
人D. 若参加书法社的人数是
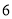 人,则该班有
人,则该班有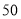 人
人
相关试题

