【题目】等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边的长为________
参考答案:
【答案】3![]() 或
或![]()
【解析】分两种情况:
(1)顶角是钝角时,如图1所示:

在Rt△ACO中,由勾股定理,得AO2=AC2-OC2=52-32=16,
∴AO=4,
OB=AB+AO=5+4=9,
在Rt△BCO中,由勾股定理,得BC2=OB2+OC2=92+32=90,
∴BC=3![]() ;
;
(2)顶角是锐角时,如图2所示:

在Rt△ACD中,由勾股定理,得AD2=AC2-DC2=52-32=16,
∴AD=4,
DB=AB-AD=5-4=1.
在Rt△BCD中,由勾股定理,得BC2=DB2+DC2=12+32=10,
∴BC=![]() ;
;
综上可知,这个等腰三角形的底的长度为3![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式减去x2-2y2等于x2-2y2 , 则这个多项式是( )
A.-2x2+2y2
B.x2-2y2
C.2x2-4y2
D.x2+2y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,﹣3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点得个数为 ;
(2)求过P点的正比例函数图象经过第二,四象限的概率(用树形图或列表法求解);
(3)过点P得正比例函数中,函数y随自变量x的增大而增大的概率为 .
-
科目: 来源: 题型:
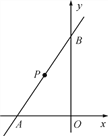
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A,B两点,且△ABO的面积为12.
(1)求k的值;
(2)若点P为直线AB上的一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形?求出此时点P的坐标;
(3)在(2)的条件下,连接PO,△PBO是等腰三角形吗?如果是,试说明理由;如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣3|﹣2= .
-
科目: 来源: 题型:
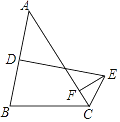
查看答案和解析>>【题目】如图,△ABC中,D是AB的中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥AC交AC于F,AC=12,BC=8,则AF=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣3,2)、B(﹣2,1)两点,现将线段AB进行平移,使点A移到坐标原点,则此时点B的坐标是_____.
相关试题

