【题目】问题背景:
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD.
CD.
简单应用:
(1)在图①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= ![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
参考答案:
【答案】
(1)3
(2)
解:连接AC、BD、AD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵ ![]() ,
,
∴AD=BD,
将△BCD绕点D,逆时针旋转90°到△AED处,如图③
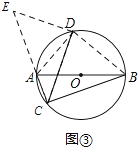 ,
,
∴∠EAD=∠DBC,
∵∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∵AB=13,BC=12,
∴由勾股定理可求得:AC=5,
∵BC=AE,
∴CE=AE+AC=17,
∵∠EDA=∠CDB,
∴∠EDA+∠ADC=∠CDB+∠ADC,
即∠EDC=∠ADB=90°,
∵CD=ED,
∴△EDC是等腰直角三角形,
∴CE= ![]() CD,
CD,
∴CD= ![]()
(3)
解:以AB为直径作⊙O,连接OD并延长交⊙O于点D1,连接D1A,D1B,D1C,如图④
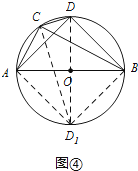
由(2)的证明过程可知:AC+BC= ![]() D1C,
D1C,
∴D1C= ![]() ,
,
又∵D1D是⊙O的直径,
∴∠DCD1=90°,
∵AC=m,BC=n,
∴由勾股定理可求得:AB2=m2+n2,
∴D1D2=AB2=m2+n2,
∵D1C2+CD2=D1D2,
∴CD=m2+n2﹣ ![]() =
= ![]() ,
,
∵m<n,
∴CD= ![]() ;
;
(4)[ "解:当点E在直线AC的左侧时,如图⑤ ![]() ,
,
连接CQ,PC,
∵AC=BC,∠ACB=90°,
点P是AB的中点,
∴AP=CP,∠APC=90°,
又∵CA=CE,点Q是AE的中点,
∴∠CQA=90°,
设AC=a,
∵AE= ![]() AC,
AC,
∴AE= ![]() a,
a,
∴AQ= ![]() AE=
AE= ![]() ,
,
由勾股定理可求得:CQ= ![]() a,
a,
由(2)的证明过程可知:AQ+CQ= ![]() PQ,
PQ,
∴ ![]() PQ=
PQ= ![]() a+
a+ ![]() a,
a,
∴ ![]() PQ=
PQ= ![]() AC;
AC;
当点E在直线AC的右侧时,如图⑥![]() 【解析】解:(1)由题意知:AC+BC=
【解析】解:(1)由题意知:AC+BC= ![]() CD,
CD,
∴3 ![]() +2
+2 ![]() =
= ![]() CD,
CD,
∴CD=3,;
(1)由题意可知:AC+BC= ![]() CD,所以将AC与BC的长度代入即可得出CD的长度;(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1 , 由(2)问题可知:AC+BC=
CD,所以将AC与BC的长度代入即可得出CD的长度;(2)连接AC、BD、AD即可将问题转化为第(1)问的问题,利用题目所给出的证明思路即可求出CD的长度;(3)以AB为直径作⊙O,连接OD并延长交⊙O于点D1 , 由(2)问题可知:AC+BC= ![]() CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.本题考查圆的综合问题,每一问都紧扣着前一问的结论,涉及勾股定理、圆周角定理,旋转的性质等知识,解题的关键是就利用好已证明的结论来进行解答,考查学生综合运用知识的能力.
CD1;又因为CD1=D1D,所以利用勾股定理即可求出CD的长度;(4)根据题意可知:点E的位置有两种,分别是当点E在直线AC的右侧和当点E在直线AC的左侧时,连接CQ、CP后,利用(2)和(3)问的结论进行解答.本题考查圆的综合问题,每一问都紧扣着前一问的结论,涉及勾股定理、圆周角定理,旋转的性质等知识,解题的关键是就利用好已证明的结论来进行解答,考查学生综合运用知识的能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
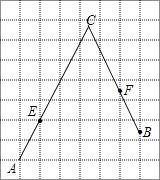
(1)AE的长等于;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1 .

(1)△A1B1C1与△ABC的位似比是;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】【操作发现】在计算器上输入一个正数,不断地按“
 ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后再x轴上确定对应的数x2 , …,以此类推.
【解决问题】研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若k=﹣ ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2 , x3 , x4 , 并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.

(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:x
…
﹣3
﹣

﹣2
﹣1
0
1
2

3
…
y
…
3

m
﹣1
0
﹣1
0

3
…
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
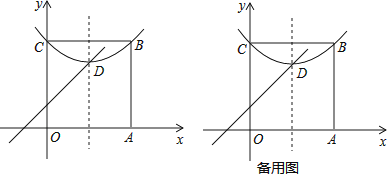
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线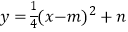 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题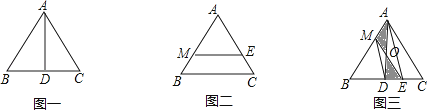
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
相关试题

