搜索
【题目】鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚 ．求笼中各有几只鸡和兔？经计算可得（ ）
A. 鸡 20 只，兔 15 只 B. 鸡 12 只，兔 23 只
C. 鸡 15 只，兔 20 只 D. 鸡 23 只，兔 12 只
参考答案：
【答案】D
【解析】
设笼中有x只鸡，y只兔，根据上有35个头、下有94只脚，即可得出关于x、y的二元一次方程组，解之即可得出结论．
设笼中有x只鸡，y只兔，根据题意得：
解得：
．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，PA、PB、AB都与⊙O相切，∠P=60°，则∠AOB等于（ ）
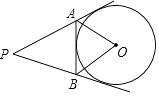
A.50°
B.60°
C.70°
D.70° -
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道1+2+3+…+
=
，则1+2+3+…+10＝ ___________ .[问题提出] 那么
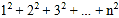的结果等于多少呢？[阅读理解] 在图1所示的三角形数阵中，第1行圆圈中的数为1，即12 ；第2行两个圆圈中数的和为2+2，即22；......；第n行n个圆圈中数的和为n+n+
n即 n2；这样，该三角形数阵中共有____ 个圆圈，所有圆圈中数的和可表示为_________________ .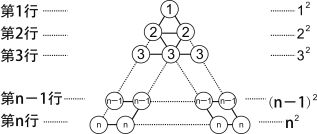 
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n－1行的第一个圆圈中的数分别为n－1，2，n）发现每个位置上三个圆圈中的数的和均为______________.由此可得，这三个三角形数阵所有圆圈中数的总和为：
3（
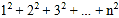）＝_________________.因此， ＝__________. 
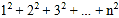图2
[问题解决]
（1）.根据以上规律可得
__________________.（2）.试计算
，请写出计算步骤. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是（ ）
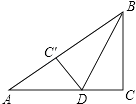
A.3cm2
B.4cm2
C.5cm2
D.6cm2 -
科目： 来源： 题型：
查看答案和解析>>【题目】函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是（ ）
A.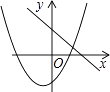
B.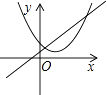
C.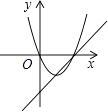
D.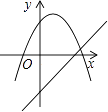
-
科目： 来源： 题型：
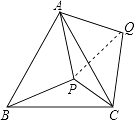
查看答案和解析>>【题目】P是等边△ABC内部一点，∠APB、∠BPC、∠CPA的大小之比是5：6：7，将△ABP逆时针旋转，使得AB与AC重合，则以PA、PB、PC的长为边的三角形的三个角∠PCQ：∠QPC：∠PQC= ．
相关试题
