【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为AC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.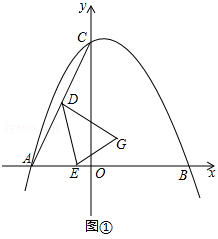
(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx+8经过点A(﹣4,0),B(6,0),
∴ ![]() ,
,
解得 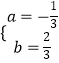 ,
,
∴抛物线的解析式是:y=﹣ ![]() x2+
x2+ ![]() x+8
x+8
(2)
解:如图1
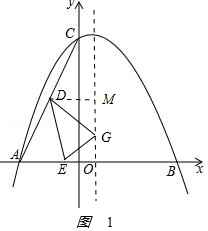 ,
,
作DM⊥抛物线的对称轴于点M,
设G点的坐标为(1,n),由翻折的性质,可得AD=DG,
∵A(﹣4,0),C(0,8),点D为AC的中点,
∴点D的坐标是(﹣2,4),
∴点M的坐标是(1,4),DM=1﹣(﹣2)=1+2=3,
∵B(6,0),C(0,8),
∴AC= ![]() =4
=4 ![]() ,
,
∴AD=2 ![]() ,
,
在Rt△GDM中,DG2=DM2+MG2
32+(4﹣n)2=20,解得n=4 ![]() ,
,
∴G点的坐标为(1,4+ ![]() )或(1,4﹣
)或(1,4﹣ ![]() )
)
(3)
解:存在.
C(0,8),D(﹣2,4),符合条件的点E、F的坐标为:
①如图2
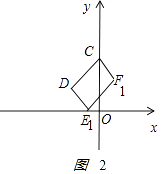 ,
,
CD∥EF,且CD=EF,CDEF时,对角线的交点(﹣ ![]() ,4),E1(﹣1,0),F1(1,4);
,4),E1(﹣1,0),F1(1,4);
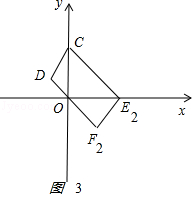
②如图3
 ,
,
CD∥EF,且CD=EF,CDFE时,对角线的交点( ![]() ,2),E2(3,0),F2(1,﹣4);
,2),E2(3,0),F2(1,﹣4);
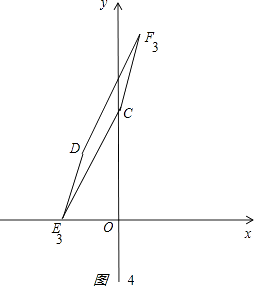
③如图4
 ,
,
DE∥CF,DE=CF,DECF时,对角线的交点(﹣1,6),E3(﹣3,0),F3(1,12).
综上所述:E1(﹣1,0),F1(1,4);E2(3,0),F2(1,﹣4);E3(﹣3,0),F3(1,12)
【解析】(1)根据待定系数法,可得函数解析式;(2)根据线段中点的性质,可得D点坐标,根据勾股定理,可得AC的长,根据翻折的性质,可得DG的长,再根据勾股定理,可得方程,根据解方程,可得答案.(3)根据平行四边形的性质,可得答案.
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
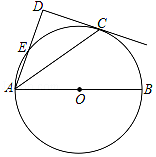
(1)求证:AC平分∠DAB;
(2)连接CE,若CE=6,AC=8,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,则这样的点至少有_____个,最多有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.
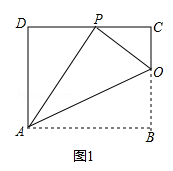
(1)求证:△HCP∽△PDA;
(2)探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.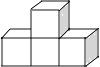
B.
C.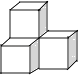
D.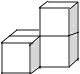
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

相关试题

