【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.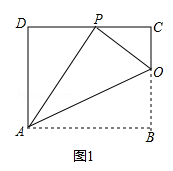
(1)求证:△HCP∽△PDA;
(2)探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
参考答案:
【答案】
(1)
解:由折叠的性质可知,
∠APH=∠B=90°,
∴∠APD+∠HPC=90°,
又∠PHC+∠HPC=90°,
∴∠APD=∠PHC,
又∠D=∠C=90°,
∴△HCP∽△PDA
(2)
解:AB=2BH.
∵HC:HB=3:5,
设HC=3x,则HB=5x,
在矩形ABCD中,BC=AD=8,
∴HC=3,则HB=5
由折叠的性质可知,HP=HB=5,AP=AB,
在Rt△HCP,根据勾股定理得,PC=4,
由(1)知,△HCP∽△PDA
∴ ![]() ,
,
∴AP= ![]() =10,
=10,
∴AB=AP=10=2BH,即AB=2BH
(3)
解:EF的长度不变.
如图,作MQ∥AB交PB于Q,

∴∠MQP=∠ABP,
由折叠的性质可知,∠APB=∠ABP,
∴∠MQP=∠APB,
∴MP=MQ,又BN=PM,
∴MQ=BN,
∵MQ∥AB,
∴ ![]() ,
,
∴QF=FB,
∵MP=MQ,ME⊥BP,
∴PE=QE,
∴EF= ![]() PB,
PB,
由(2)得,PC=4,BC=8,
∴PB= ![]() =4
=4 ![]() ,
,
∴EF=2 ![]()
【解析】(1)先利用等角的余角相等得出∠APD=∠PHC,即可得出结论;(2)先求出HC=3,HB=5,进而得出HP=5,再用勾股定理求出PC,最后用△HCP∽△PDA得出的比例式即可得出结论;(3)先判断出MQ=BN,进而得出QF=FB,再判断出EF= ![]() PB,最后用勾股定理求出PB即可得出结论.
PB,最后用勾股定理求出PB即可得出结论.
【考点精析】掌握勾股定理的概念和翻折变换(折叠问题)是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.
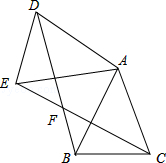
(1)求证:△AEC≌△ADB;
(2)若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
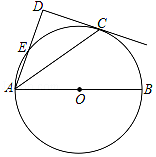
(1)求证:AC平分∠DAB;
(2)连接CE,若CE=6,AC=8,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,则这样的点至少有_____个,最多有_____个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为AC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
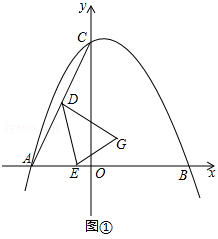
(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )

A. 得分在70~80分之间的人数最多
B. 该班的总人数为40
C. 得分在90~100分之间的人数最少
D. 及格(≥60分)人数是26
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A.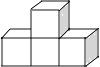
B.
C.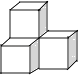
D.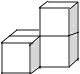
相关试题

