Question

【题目】如图，AB和CD分别是⊙O上的两条弦，过点O分别作ON⊥CD于点N，OM⊥AB于点M，若ON=AB，证明：OM=CD．

Answer 1

【答案】证明：设圆的半径是r，ON=x，则AB=2x，
在直角△CON中，CN==，
∵ON⊥CD，
∴CD=2CN=2，
∵OM⊥AB，
∴AM=AB=x，
在△AOM中，OM==，
∴OM=CD．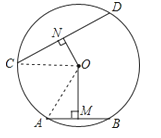

【解析】设圆的半径是r，ON=x，则AB=2x，在直角△CON中利用勾股定理即可求得CN的长，然后根据垂径定理求得CD的长，然后在直角△OAM中，利用勾股定理求得OM的长，即可证得．
【考点精析】根据题目的已知条件，利用垂径定理的相关知识可以得到问题的答案，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．