【题目】如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM.
求证:(1)四边形AMCF是菱形;
(2)△ACB≌△MCE.

参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】分析:(1)、利用等边三角形的判定与性质得出∠ACB=∠FAC,进而求出四边形AMCF是平行四边形,再得出△AMC是等边三角形,即可得出答案;(2)、利用等边三角形的性质结合全等三角形的判定方法得出即可.
详解:(1)、∵△ACF是等边三角形,∴∠FAC=∠ACF=60°,AC=CF=AF, ∵∠ACB=60°,
∴∠ACB=∠FAC, ∴AF∥BC, ∵AM∥FC, ∴四边形AMCF是平行四边形,
∵AM∥FC,∠ACB=∠ACF=60°, ∴∠AMC=60°, 又∵∠ACB=60°,
∴△AMC是等边三角形, ∴AM=MC, ∴四边形AMCF是菱形;
(2)、∵△BCE是等边三角形, ∴BC=EC,
在△ABC和△MEC中∵ , ∴△ABC≌△MEC(SAS).
, ∴△ABC≌△MEC(SAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】你能找出规律吗?
(1)计算:
 ×
× =________,
=________, =________;
=________; ×
×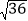 =________,
=________, =________.
=________.(2)请按找到的规律计算:
①
 ×
× ;
;②
 ×
× .
.(3)已知a=
 ,b=
,b= ,用含a,b的式子表示
,用含a,b的式子表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC与△A1B1C1 , 关于点E成中心对称.
(1)画出对称中心E,并写出点E的坐标是 ;
(2)P(a,b)是边上的一点,△ABC经过平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2 . 并写出点A2坐标为 ,点B2坐标为 ;
(3)直接判断并写出△A1B1C1 , 与△A2B2C2的位置关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=
 AB,证明:OM=
AB,证明:OM= CD.
CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有2个信封A、B,信封A装有四张卡片上分别写有1、2、3、4,信封B装有三张卡片分别写有5、6、7,每张卡片除了数字没有任何区别.从这两个信封中随机抽取两张卡片.
(1)请你用列表法或画树状图的方法描述所有可能的结果;
(2)把卡片上的两个数相加,求“得到的和是3的倍数”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

相关试题

