搜索
【题目】已知四边形ABCD的对角线AC=8
，BD=6
，且
，P、Q、R、S分别是AB、BC、CD、DA的中点，则PR2+QS2的值是__________．
参考答案：
【答案】118
【解析】
连接PQ，QR，RS，SQ，易证四边形PQRS是平行四边形，因为AC⊥BD，所以PQ⊥QR，所以四边形PQRS为矩形，进而可得PR2+QS2=PQ2+QR2+QR2+SR2=118，问题得解．
连接PQ，QR，RS，SQ，
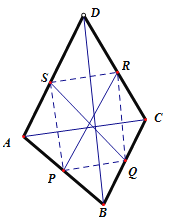
P、Q、R、S分别是AB、BC、CD、DA的中点，
∴
∴PS∥BD,
QR∥BD,
∴四边形PQRS是平行四边形，
∵AC⊥BD，
∴PQ⊥QR，
∴四边形PQRS为矩形，
∴PR2+QS2=PQ2+QR2+QR2+SR2=
=118，
故答案为：118
-
科目： 来源： 题型：
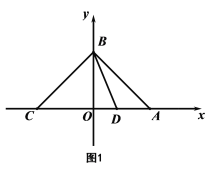
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A(a，0)，B(0，b)，C（-a，0），且
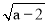+b2-4b+4=0．(1)求证：∠ABC=90°；
(2)∠ABO的平分线交x轴于点D，求D点的坐标．
(3)如图，在线段AB上有两动点M、N满足∠MON=45°，求证：BM2+AN2=MN2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH=DF，连接AH、FH，FH与AC交于点M，以下结论：
①FH=2BH；②AC⊥FH；③S△ACF=1；④CE=
AF；⑤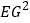
=FGDG，其中正确结论的个数为（ ）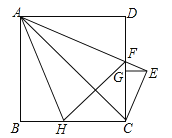
A. 2 B. 3 C. 4 D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知M是△ABC的边AB的中点，D是MC的延长线上一点，满足∠ACM=∠BDM．
(1)求证：AC=BD；
(2)若∠BMC=60°，求
的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【题目】如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝
(k≠0)的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH＝3，tan∠AOH＝
，点B的坐标为(m，－2)．(1)求△AHO的周长；
(2)求该反比例函数和一次函数的解析式．
-
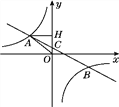
科目： 来源： 题型：
查看答案和解析>>【题目】如图是单位长度为1的正方形网格，若A，B两点的坐标分别为
，
.
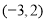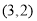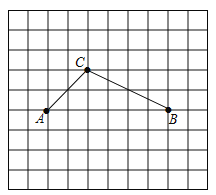
请解决下列问题：
（1）在网格图中画出平面直角坐标系，并直接写出点C的坐标_________.
（2）将图中三角形ABC沿x轴向右平移1个单位，再沿y轴向上平移2个单位后得到三角形
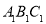，则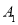
的坐标为_________；
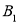的坐标为_________；
的坐标为_________；（3）在y轴上是否存在点P，使得三角形
的面积为4，若存在，请直接写出P点坐标：若不存在，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】某学校要开展校园艺术节活动，为了合理编排节目，对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查（每名学生必须选择且只能选择一类），并将调查结果绘制成如下两幅不完整的统计图.
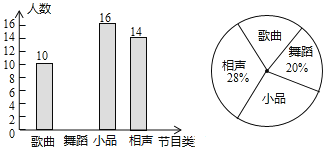
请根据图中信息，回答下列问题：
（1）本次共调查了_________名学生.
（2）在扇形统计图中，“歌曲”所在扇形的圆心角等于_________度.
（3）补全条形统计图（并标注频数）.
（4）根据以上统计分析，估计该校2000名学生中最喜爱小品的人数约有多少名？
相关试题
