【题目】某学校要开展校园艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下两幅不完整的统计图.
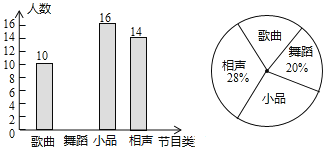
请根据图中信息,回答下列问题:
(1)本次共调查了_________名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于_________度.
(3)补全条形统计图(并标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数约有多少名?
参考答案:
【答案】(1)50;(2)72;(3)图略;(4)2000名学生中最喜爱小品的人数约有640名.
【解析】
(1)从两个统计图中可得喜欢“相声”的人数为14人,占调查人数的28%,可求出调查人数;
(2)用360°乘以样本中“歌曲”所占的比即可;
(3)计算出喜欢“舞蹈”人数,再补全条形统计图;
(4)样本估计总体,用总人数2000乘以样本中“小品”所占的比.
(1)14÷28%=50(名).
故答案为:50.
(2)360°![]() 72°.
72°.
故答案为:72.
(3)50﹣10﹣16﹣14=10(名),补全条形统计图如图所示:
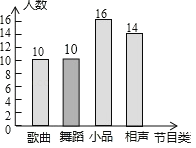
(4)2000![]() 640(名).
640(名).
答:该校2000名学生中最喜爱小品的人数约有640名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC=8
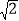 ,BD=6
,BD=6 ,且
,且 ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________. -
科目: 来源: 题型:
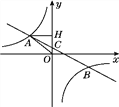
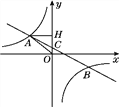
查看答案和解析>>【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是单位长度为1的正方形网格,若A,B两点的坐标分别为
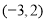 ,
,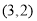 .
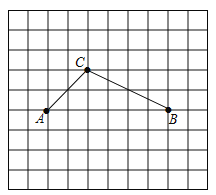
.
请解决下列问题:
(1)在网格图中画出平面直角坐标系,并直接写出点C的坐标_________.
(2)将图中三角形ABC沿x轴向右平移1个单位,再沿y轴向上平移2个单位后得到三角形
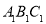 ,则
,则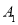 的坐标为_________;
的坐标为_________;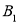 的坐标为_________;
的坐标为_________;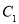 的坐标为_________;
的坐标为_________;(3)在y轴上是否存在点P,使得三角形
 的面积为4,若存在,请直接写出P点坐标:若不存在,请说明理由.
的面积为4,若存在,请直接写出P点坐标:若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
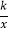 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=
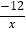 ,一次函数的解析式为y=-
,一次函数的解析式为y=- x+1.
x+1.【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=
 ,得
,得AH=4.即A(-4,3).
由勾股定理,得
AO=
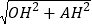 =5,
=5,△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=
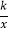 (k≠0),得
(k≠0),得k=-4×3=-12,
反比例函数的解析式为y=
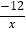 ;
;当y=-2时,-2=
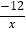 ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).将A、B点坐标代入y=ax+b,得
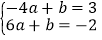 ,
,解得
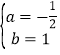 ,
,一次函数的解析式为y=-
 x+1.
x+1.考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
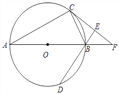
21【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
-
科目: 来源: 题型:
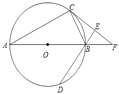
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
【答案】30°
【解析】(1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.答:
(1)证明:连结OC,如图,
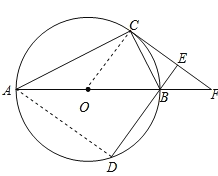
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时,四边形ACFD是菱形,理由如下:
∵∠A=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠A=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
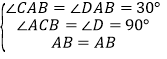 ,
,∴△ACB≌△ADB,
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形。
故答案为:30°.
【题型】解答题
【结束】
22【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.

(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?直接写出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若化简|1-x|-
 的结果为2x﹣5,则x的取值范围是( )
的结果为2x﹣5,则x的取值范围是( )A. x为任意实数B. 1≤x≤4 C. x≥1D. x≤4
相关试题

