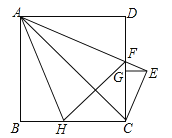
【题目】如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:
①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=![]() AF;⑤
AF;⑤![]() =FGDG,其中正确结论的个数为( )
=FGDG,其中正确结论的个数为( )
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
【解析】①②如图1,∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,∠BAD=90°,∵AE平分∠DAC,∴∠FAD=∠CAF=22.5°,∵BH=DF,∴△ABH≌△ADF,∴AH=AF,∠BAH=FAD=22.5°,∴∠HAC=∠FAC,∴HM=FM,AC⊥FH,∵AE平分∠DAC,∴DF=FM,∴FH=2DF=2BH,故选项①②正确;
③在Rt△FMC中,∠FCM=45°,∴△FMC是等腰直角三角形,∵正方形的边长为2,∴AC=![]() ,MC=DF=
,MC=DF=![]() ﹣2,∴FC=2﹣DF=2﹣(
﹣2,∴FC=2﹣DF=2﹣(![]() ﹣2)=4﹣
﹣2)=4﹣![]() ,S△AFC=
,S△AFC=![]() CFAD≠1,所以选项③不正确;
CFAD≠1,所以选项③不正确;
④AF=![]() =
=![]() =
=![]() ,∵△ADF∽△CEF,∴
,∵△ADF∽△CEF,∴![]() ,∴
,∴![]() ,∴CE=
,∴CE=![]() ,∴CE=
,∴CE=![]() AF,故选项④正确;
AF,故选项④正确;
⑤在Rt△FEC中,EG⊥FC,∴![]() =FGCG,cos∠FCE=
=FGCG,cos∠FCE=![]() ,∴CG=
,∴CG=![]() =
=![]() =1,∴DG=CG,∴
=1,∴DG=CG,∴![]() =FGDG,故选项⑤正确;
=FGDG,故选项⑤正确;
本题正确的结论有4个,
故选C.

-
科目: 来源: 题型:
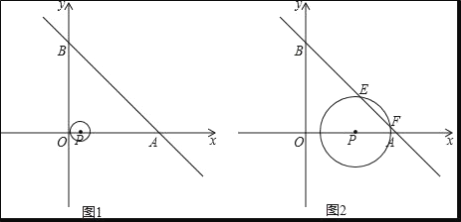
查看答案和解析>>【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=
 时,弦EF的长;
时,弦EF的长;②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.


-
科目: 来源: 题型:
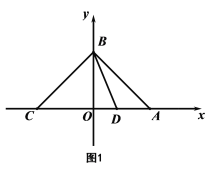
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且
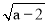 +b2-4b+4=0.
+b2-4b+4=0.(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC=8
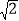 ,BD=6
,BD=6 ,且
,且 ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________. -
科目: 来源: 题型:
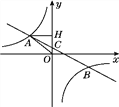
查看答案和解析>>【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
相关试题

