【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,
,![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用配方法求出抛物线的顶点坐标是(m,-m+1),根据顶点在x轴上,得出-m+1=0,求出m=1,即可得出抛物线的解析式;(2)由于抛物线的顶点坐标是(m,-m+1),即可得出顶点在直线y=-x+1上;(3)把点A(-1,0)代入![]() 求出m的值,再把B(1,0)代入
求出m的值,再把B(1,0)代入![]() 求出m的值,即可求得m的取值范围.
求出m的值,即可求得m的取值范围.
![]() ∵
∵![]() ,
,
∴顶点坐标是![]() ,
,
∵抛物线的顶点在![]() 轴上,
轴上,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() ∵抛物线
∵抛物线![]() 的顶点坐标是
的顶点坐标是![]() ,
,
∴抛物线的顶点在直线![]() 上;
上;
![]() 当抛物线
当抛物线![]() 过点
过点![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
当抛物线![]() 过点
过点![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售某种玩具,进货价为
 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是 元时,销售量是
元时,销售量是 件,而销售单价每上涨
件,而销售单价每上涨 元,就会少售出
元,就会少售出 件玩具,超市要完成不少于
件玩具,超市要完成不少于 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点
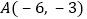 .
. 写出函数表达式;
写出函数表达式; 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限? 随
随 的增大怎样变化?
的增大怎样变化? 点
点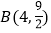 、
、 在这个函数的图象上吗?
在这个函数的图象上吗? 如果点
如果点 在图象上,求
在图象上,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
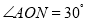 ,点P是射线ON上一动点,点B是射线OA上一动点,点B,P均不与点O重合,当
,点P是射线ON上一动点,点B是射线OA上一动点,点B,P均不与点O重合,当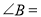 _____时,
_____时,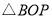 为直角三角形;如果使得
为直角三角形;如果使得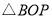 为钝角三角形,则
为钝角三角形,则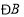 的取值范围是_____.
的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为
的边长为 ,点
,点 为
为 上的一点,点
上的一点,点 为
为 上的一点,
上的一点,连结
 、
、 ,
, .
.
 求证:①
求证:① ;②
;② ;
; 若
若 ,求
,求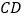 和
和 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.

相关试题

