【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 上的一点,点
上的一点,点![]() 为
为![]() 上的一点,
上的一点,
连结![]() 、
、![]() ,
,![]() .
.

![]() 求证:①
求证:①![]() ;②
;②![]() ;
;
![]() 若
若![]() ,求
,求![]() 和
和![]() 的长.
的长.
参考答案:
【答案】(1) ①见解析; ②见解析;(2)![]() ,
,![]() .
.
【解析】
(1)①由△ABC为等边三角形,可得∠B=∠C=60°,又∠APD=60°,由三角形外角的性质可得∠DPC=∠PAB,根据两角对应相等的两个三角形相似即可得△ABP∽△PCD;②利用两角对应相等的两个三角形相似证明△ADP∽△APC,根据相似三角形的性质即可证得结论;(2)由(1)知△ABP∽△PCD,根据相似三角形的性质可得AB:PC=BP:CD,代入数据求得CD的长,即可得AD的长,再利用AP2=ADAC求得AP的长即可.
![]() 证明:①在等边三角形
证明:①在等边三角形![]() 中,
中,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;![]() 解:∵
解:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵等边三角形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线
 当抛物线的顶点在
当抛物线的顶点在 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式; 不论
不论 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式; 若有两点
若有两点 ,
, ,且该抛物线与线段
,且该抛物线与线段 始终有交点,请直接写出
始终有交点,请直接写出 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
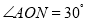 ,点P是射线ON上一动点,点B是射线OA上一动点,点B,P均不与点O重合,当
,点P是射线ON上一动点,点B是射线OA上一动点,点B,P均不与点O重合,当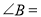 _____时,
_____时,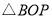 为直角三角形;如果使得
为直角三角形;如果使得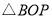 为钝角三角形,则
为钝角三角形,则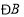 的取值范围是_____.
的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法: ①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ①②③④ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了
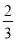 ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
相关试题

