【题目】如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=52°,
∠F=26°.
(1)求证:EG⊥BD;(2)求∠CDB的度数.

参考答案:
【答案】(1)见解析;(2)116°;
【解析】分析: (1)根据平行线的性质得到∠BED=∠CDE=52°,由角平分线的定义得到∠DEG=26°,然后根据平行线的性质即可得到结论;
(2)由(1)得∠FBE=∠BEG=26°,根据平行线的性质即可得到结论.
详解: :(1)∵AB∥CD,∠CDE=52°,
∴∠BED=∠CDE=52°,
∵EG平分∠DEB,
∴∠DEG=26°,
∵∠F=26°,
∴BF∥EG,
∵FB⊥BD,
∴EG⊥BD;
(2)由(1)得∠FBE=∠BEG=26°,
∵∠FBD=90°,
∴∠EBD=64°,
∵AB∥CD,
∴∠CDB=116°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板按如图所示叠放在一起,若固定
 ,将
,将 绕着公共顶点
绕着公共顶点 ,按顺时针方向旋转
,按顺时针方向旋转 度
度 ,当
,当 的一边与
的一边与 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角 的度数为_________________。
的度数为_________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A. 2 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
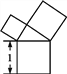

图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
相关试题

