搜索
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
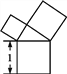
图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
参考答案：
【答案】D
【解析】解：设直角三角形的三条边分别是a，b，c．根据勾股定理，得：a2+b2=c2，即正方形A的面积+正方形B的面积=正方形C的面积=1．推而广之，“生长”了2017次后形成的图形中所有的正方形的面积和是2018×1=2018．故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD被直线BD，DF所截，AB∥CD，FB⊥DB，垂足为B，EG平分∠DEB，∠CDE=52°，
∠F=26°.
(1)求证：EG⊥BD；(2)求∠CDB的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠BAP+∠APD=180°，∠1=∠2，求证：∠E=∠F．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB＝90°，分别以点A和点B为圆心，以相同的长（大于
AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E．若AC＝3，AB＝5，则DE等于（ ）
A. 2 B.
C. 
D. 
-
科目： 来源： 题型：
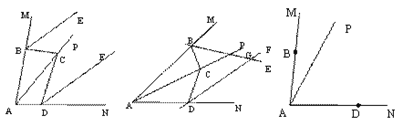
查看答案和解析>>【题目】已知，点B、D分别在∠MAN的两边AM、AN上，点C是射线AP上的一点，连接BC、DC，∠MAN=α，∠BCD=β，(0°＜α＜180°，0°＜β＜180°)；BE平分∠MBC，DF平分∠NDC.
(1)如图1，若α=β=80°，
①求∠MBC+∠NDC的度数；
②判断BE、DF的位置关系，并说明理由.
(2)如图2，当点C在射线AP上运动时，若直线BE、DF相交于点G，请用含有α、β的代数式表示∠BGD.(直接写结果)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AB=21,AD=9.求AC的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）在直角坐标系中描出下列各点A（2，1），B（-2，1），C（3，2），D（-3，2）；
（2）连结AB、CD观察它们与y轴的关系，
（3）猜想（a，1）(-a，1)两点的连线是否遵循上述规律.
相关试题
