【题目】如图,数轴上有 A、B 两点,所表示的有理数分别为 a、b,已知 AB=12,原点 O 是线段AB 上的一点,且 OA=2OB.
![]()
(1)求a,b;
(2)若动点 P,Q 分别从 A,B 同时出发,向右运动,点 P 的速度为每秒 2 个单位长度,点 Q 的速度为每秒 1 个单位长度,设运动时间为 t 秒,当点 P 与点 Q 重合时,P,Q 两点停止运动.
①当 t 为何值时,2OPOQ=4;
②当点 P 到达点 O 时,动点 M 从点 O 出发,以每秒 3 个单位长度的速度也向右运动,当点 M 追上点 Q 后立即返回,以同样的速度向点 P 运动,遇到点 P 后再立即返回,以同样的速度向点 Q 运动,如此往返,直到点 P,Q 停止时,点 M 也停止运动,求在此过程中点 M 行驶的总路程,并直接写出点 M 最后位置在数轴上所对应的有理数.
参考答案:
【答案】(1)a=-8,b=4;(2)①当 t 为 1.6 秒或 8 秒时,2OP-OQ=4;②点 M 行驶的总路程为 24 和点 M 最后位置在数轴上对应的实数为16.
【解析】
(1)由AO=2OB可知,将12平均分成三份,AO占两份为8,OB占一份为4,由图可知,A在原点的左边,B在原点的右边,从而得出结论;
(2)①分两种情况:点P在原点的左侧和右侧时,OP表示的代数式不同,OQ=4+t,分别代入2OP﹣OQ=4列式即可求出t的值;
②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为t秒,列式为t(2﹣1)=8,解出即可解决问题.
(1)∵AB=12,AO=2OB,∴AO=8,OB=4,∴A点所表示的实数为﹣8,B点所表示的实数为4,∴a=﹣8,b=4.
故答案为:﹣8;4;
(2)①当0<t≤4时,如图3,AP=2t,OP=8﹣2t,BQ=t,OQ=4+t.

∵2OP﹣OQ=4,∴2(8﹣2t)﹣(4+t)=4,t=![]() =1.6;
=1.6;
当点P与点Q重合时,如图4,2t=12+t,t=12;
当4<t<12时,如图5,OP=2t﹣8,OQ=4+t,则2(2t﹣8)﹣(4+t)=4,t=8.

综上所述:当t为1.6秒或8秒时,2OP﹣OQ=4;
②当点P到达点O时,8÷2=4,此时,OQ=4+t=8,即点Q所表示的实数为8,如图6,设点M运动的时间为t秒,由题意得:2t﹣t=8,t=8,此时,点P表示的实数为8×2=16,所以点M表示的实数也是16,∴点M行驶的总路程为:3×8=24.
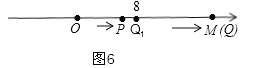
答:点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.
-
科目: 来源: 题型:
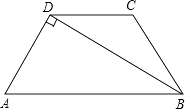
查看答案和解析>>【题目】如图所示,在梯形ABCD中,AB∥DC,BD⊥AD,AD=DC=BC=2cm,那么梯形ABCD的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离cm.
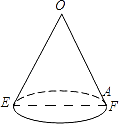
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

-
科目: 来源: 题型:
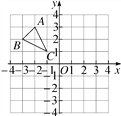
查看答案和解析>>【题目】如图,格点△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC先向下平移4个单位长度,再向右平移3个单位长度,画出平移后的△A1B1C1,并写出顶点B1的坐标;
(2)作△ABC关于y轴的对称图形△A2B2C2,并写出顶点B2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求完成下列题目:
(1)图中有 块小正方体;
(2)请在下面方格纸中分别画出它的主视图,左视图和俯视图.

(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
相关试题

