【题目】如图,在△ABC中,BC=4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是(结果保留π). 
参考答案:
【答案】4﹣ ![]()
【解析】解:连接AD,则AD⊥BC; 
△ABC中,BC=4,AD=2;
∴S△ABC= ![]() BCAD=4.
BCAD=4.
∵∠EAF=2∠EPF=80°,AE=AF=2;
∴S扇形EAF= ![]() =
= ![]() ;
;
∴S阴影=S△ABC﹣S扇形EAF=4﹣ ![]() .
.
【考点精析】利用圆周角定理和切线的性质定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的.设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分钟)之间的函数关系如图所示.根据图象信息给出下列说法:①每分钟进水5升;②当4≤x≤12时,容器中的水量在减少;③若12分钟后只放水,不进水,还要8分钟可以把水放完;④若从一开始进出水管同时打开,则需要24分钟可以将容器灌满.其中正确的有________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,解是x=﹣
 的是( )
的是( )A. 3(x-
 )=0 B. 2x﹣(x+1)=0 C.
)=0 B. 2x﹣(x+1)=0 C.  D.
D. 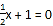
-
科目: 来源: 题型:
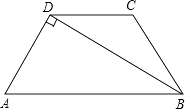
查看答案和解析>>【题目】如图所示,在梯形ABCD中,AB∥DC,BD⊥AD,AD=DC=BC=2cm,那么梯形ABCD的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离cm.
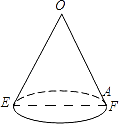
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有 A、B 两点,所表示的有理数分别为 a、b,已知 AB=12,原点 O 是线段AB 上的一点,且 OA=2OB.

(1)求a,b;
(2)若动点 P,Q 分别从 A,B 同时出发,向右运动,点 P 的速度为每秒 2 个单位长度,点 Q 的速度为每秒 1 个单位长度,设运动时间为 t 秒,当点 P 与点 Q 重合时,P,Q 两点停止运动.
①当 t 为何值时,2OPOQ=4;
②当点 P 到达点 O 时,动点 M 从点 O 出发,以每秒 3 个单位长度的速度也向右运动,当点 M 追上点 Q 后立即返回,以同样的速度向点 P 运动,遇到点 P 后再立即返回,以同样的速度向点 Q 运动,如此往返,直到点 P,Q 停止时,点 M 也停止运动,求在此过程中点 M 行驶的总路程,并直接写出点 M 最后位置在数轴上所对应的有理数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

相关试题

