【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 
参考答案:
【答案】![]()
a
【解析】解:如图,连接OE、OF,
∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴OECF是正方形,
∵由△ABC的面积可知 ![]() ×AC×BC=
×AC×BC= ![]() ×AC×OE+
×AC×OE+ ![]() ×BC×OF,
×BC×OF,
∴OE=OF= ![]() a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
a=EC=CF,BF=BC﹣CF=0.5a,GH=2OE=a,
∵由切割线定理可得BF2=BHBG,
∴ ![]() a2=BH(BH+a),
a2=BH(BH+a),
∴BH= ![]() a或BH=
a或BH= ![]() a(舍去),
a(舍去),
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴ ![]() =
= ![]() ,
,
∴BH=BD,CD=BC+BD=a+ ![]() a=
a= ![]() a.
a.
故答案为: ![]() a.
a.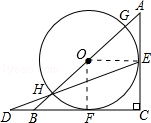
连接OE、OF,由切线的性质结合结合直角三角形可得到正方形OECF,并且可求出⊙O的半径为0.5a,则BF=a﹣0.5a=0.5a,再由切割线定理可得BF2=BHBG,利用方程即可求出BH,然后又因OE∥DB,OE=OH,利用相似三角形的性质即可求出BH=BD,最终由CD=BC+BD,即可求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(-P)2·(-P)3=_________
(2)若xm=x2×(-x)4,则m=__________
(3)若a3·am=a9,则m=__________
(4)计算22012-22013=__________
-
科目: 来源: 题型:
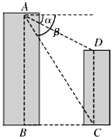
查看答案和解析>>【题目】如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为m(结果不作近似计算).
-
科目: 来源: 题型:
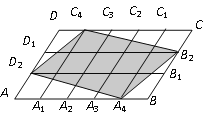
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
A. 4 B.
 C.
C.  D. 30
D. 30 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3
 ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+ .其中正确的结论是
.其中正确的结论是
A. ①②③⑤ B. ①③④ C. ②③④⑤ D. ①②⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程
 的两个实数根,则△ABC的周长为___.
的两个实数根,则△ABC的周长为___. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:2sin60°﹣( )﹣1+(
)﹣1+( 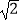 ﹣1)0
﹣1)0
(2)先化简,再求值:(1﹣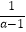 )÷
)÷ 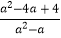 ,其中a=2+
,其中a=2+ 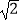 .
.
相关试题

