【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为 . 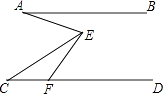
参考答案:
【答案】36°或37°
【解析】解:如图,过E作EG∥AB,
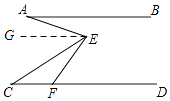
∵AB∥CD,
∴GE∥CD,
∴∠BAE=∠AEG,∠DFE=∠GEF,
∴∠AEF=∠BAE+∠DFE,
设∠CEF=x,则∠AEC=2x,
∴x+2x=∠BAE+60°,
∴∠BAE=3x﹣60°,
又∵6°<∠BAE<15°,
∴6°<3x﹣60°<15°,
解得22°<x<25°,
又∵∠DFE是△CEF的外角,∠C的度数为整数,
∴∠C=60°﹣23°=37°或∠C=60°﹣24°=36°,
所以答案是:36°或37°.
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线
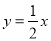 于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和
于点B1,以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2∥y轴,分别交直线y=x和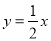 于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)
于A2,B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为 .(用含正整数n的代数式表示)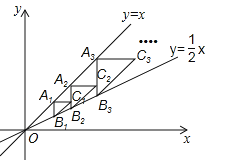
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的三边长分别为3,4,x,则x2为( )
A. 5 B. 25 C. 7 D. 7或25
-
科目: 来源: 题型:
查看答案和解析>>【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α=55.5°,∠β=55°5',那么∠α与∠β之同的大小关系是( )
A. ∠α>∠β B. ∠α<∠β C. ∠α=∠β D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)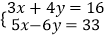
(2)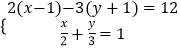 .
.
相关试题

