【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)
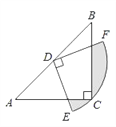
参考答案:
【答案】![]()
【解析】连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=![]() AB=
AB=![]() ,四边形DMCN是正方形,DM=1.
,四边形DMCN是正方形,DM=1.
则扇形FDE的面积=![]() .
.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
在△DMG和△DNH中,
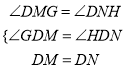 ,
,
∴△DMG≌△DNH(AAS),
∴![]() .
.
∴阴影部分的面积=![]() 1.
1.
故答案为: ![]() 1.
1.
-
科目: 来源: 题型:
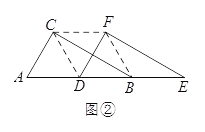
查看答案和解析>>【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF进行如下操作:
(1)操作发现
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC,CF,FB,四边形CDBF的形状在不断的变化,那么它的面积大小是否变化呢?如果不变化,请求出其面积.
(2)猜想论证
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展探究
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,求sin
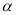

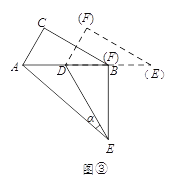
-
科目: 来源: 题型:
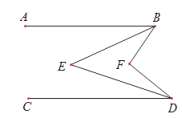
查看答案和解析>>【题目】如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上海与杭州的实际距离约200千米,在比例尺为1:5000000的地图上,上海与杭州的图上距离约 厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB

-
科目: 来源: 题型:
查看答案和解析>>【题目】增城市4月份前5天的最高气温如下(单位:℃):27,30,24,30,31,对这组数据,下列说法正确的是( )
A.平均数为28
B.众数为30
C.中位数为24
D.方差为5 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣20)+16的结果是( )
A.﹣4
B.4
C.﹣2016
D.2016
相关试题

