【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF进行如下操作:
(1)操作发现
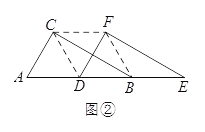
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC,CF,FB,四边形CDBF的形状在不断的变化,那么它的面积大小是否变化呢?如果不变化,请求出其面积.
(2)猜想论证
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展探究
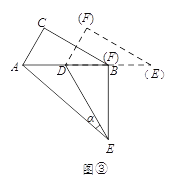
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,求sin![]()

参考答案:
【答案】(1)不变,8![]() (2)菱形,理由见解析;(3)
(2)菱形,理由见解析;(3)![]()
【解析】(1)不变 8![]() (2)菱形,理由略) (3)
(2)菱形,理由略) (3) ![]()
-
科目: 来源: 题型:
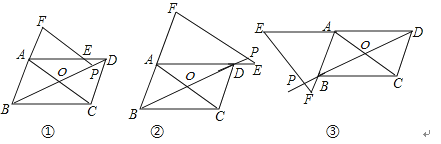
查看答案和解析>>【题目】已知平行四边形ABCD的对角线交于点O,点P是直线BD上任意一点(异于B、O、D三点),过P点作平行于AC的直线交直线AD于点E,交直线BA于点F,当点P在线段BD上时,易证得:AC=PE+PF(如图①所示).当点P在线段BD的延长线上(如图②所示)和当点P在线段DB的延长线上(如图③所示)两种情况时,探究线段AC、PE、PF之间的数量关系,并对图③的结论进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解中低收入人群和新参加工作的大学生住房的需求,某市将新建保障住房3600000套,把3600000用科学记数法表示应是( )
A.0.36×107
B.3.6×106
C.3.6×107
D.36×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O1的半径R1=4,⊙O2的半径R2=2,且两圆圆心距O1O2=1,则此两圆的位置关系是( )
A.相交B.相切C.外离D.内含
-
科目: 来源: 题型:
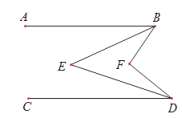
查看答案和解析>>【题目】如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上海与杭州的实际距离约200千米,在比例尺为1:5000000的地图上,上海与杭州的图上距离约 厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=
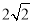 ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为________(结果保留π)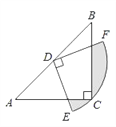
相关试题

