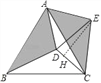
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E.
(1)DE=_____;
(2)∠CDE的正切值为_____.

参考答案:
【答案】 5, 3![]()
【解析】分析:(1)先利用等边三角形的性质AB=AC,∠BAC=60°,再根据旋转的性质得AD=AE, ∠DAE=∠BAC=60°,CE=BD=6,然后判断△ADE为等边三角形得到DE的长;(2) 作EH⊥CD于H, 设DH=x,则CH=4﹣x,利用勾股定理得到52﹣x2=62﹣(4-x),解得x=![]() ,再计算出EH的长,然后利用正切的定义求解.
,再计算出EH的长,然后利用正切的定义求解.
详解:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴AD=AE,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5;
(2)作EH⊥CD于H,如图,
设DH=x,则CH=4﹣x,
在Rt△EDH中,EH2=DE2﹣DH2=52﹣x2,
在Rt△ECH中,EH2=CE2﹣CH2=62﹣(4﹣x)2,
∴52﹣x2=62﹣(4﹣x)2,解得x=![]() ,
,
∴EH=![]() =
=![]() ,
,
∴tan∠EDH=![]() =3
=3![]() ,
,
即∠CDE的正切值为3![]() .
.
故答案为5,3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市要销售一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价为多少元时,该文具每天的销售利润最大,并求出最大的利润;
(2)经过试营销后,超市按(1)中单价销售,为了回馈广大顾客,同时提高该文具知名度,超市决定在1月1日当天开展降价促销活动,若每件文具降价2a%,则可多售出4a%,结果当天销售额为5670元,要使销量尽可能地大,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于
 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.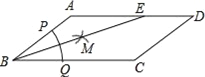
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,△ADC和△BDE均为等腰三角形,∠CAD=∠DBE,AC=AD,BD=BE,连接CE,点G为CE的中点,过点E作AC的平行线与线段AG延长线交于点F.
(1)当A,D,B三点在同一直线上时(如图1),求证:G为AF的中点;
(2)将图1中△BDE绕点D旋转到图2位置时,点A,D,G,F在同一直线上,点H在线段AF的延长线上,且EF=EH,连接AB,BH,试判断△ABH的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE=CE.
(1)用尺规或只用无刻度的直尺作出
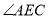 的角平分线,保留作图痕迹,不需要写作法.
的角平分线,保留作图痕迹,不需要写作法.(2)设
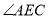 的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.
的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.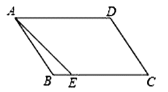
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
相关试题

