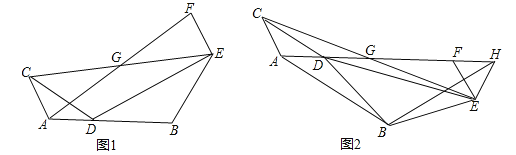
【题目】已知如图,△ADC和△BDE均为等腰三角形,∠CAD=∠DBE,AC=AD,BD=BE,连接CE,点G为CE的中点,过点E作AC的平行线与线段AG延长线交于点F.
(1)当A,D,B三点在同一直线上时(如图1),求证:G为AF的中点;
(2)将图1中△BDE绕点D旋转到图2位置时,点A,D,G,F在同一直线上,点H在线段AF的延长线上,且EF=EH,连接AB,BH,试判断△ABH的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)△ABH为等腰三角形.理由见解析.
【解析】试题分析:(1)依据AC∥EF,可得∠ACG=∠FEG,根据点G为CE的中点,可得CG=EG,再根据∠AGC=∠FGE,即可得出△ACG≌△FEG,进而得到G为AF的中点;
(2)依据△ACG≌△FEG,可得AC=FE,再根据AC=AD,FE=HE,即可得到AD=HE,运用四边形内角和以及同角的补角相等可得∠BEH=∠BDA,再根据BD=BE,即可得到△ADB≌△HEB,可得AB=HB,即△ABH是等腰三角形.
试题解析:解:(1)∵AC∥EF,∴∠ACG=∠FEG.∵点G为CE的中点,∴CG=EG.又∵∠AGC=∠FGE,∴△ACG≌△FEG,∴AG=FG,∴G为AF的中点;
(2)△ABH为等腰三角形.理由如下:
同(1)可证△ACG≌△FEG,∴AC=FE.又∵AC=AD,FE=HE,∴AD=HE,①
∵AC∥EF,∴∠GFE=∠CAD=∠DBE.∵EF=EH,∴∠EFH=∠EHF.∵∠EFH+∠GFE=180°,∴∠FHE+∠DBE=180°,∴四边形BDHE中,∠BEH+∠BDF=180°.又∵∠BDA+∠BDF=180°,∴∠BEH=∠BDA,②
又∵BD=BE,③
∴由①②③,可得△ADB≌△HEB,∴AB=HB,即△ABH是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明有5张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题:
(1)从中取出3张卡片,使这3张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M,以下结论:
①△BCD是等腰三角形;②射线CD是∠ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD。
正确的有( )

A. ①② B. ①③ C. ①②③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O……依此规律,得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标( )
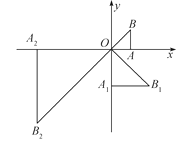
A. (22 017,-22 017) B. (22 016,-22 016) C. (22 017,22 017) D. (22 016,22 016)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
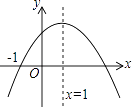
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
相关试题

