【题目】如图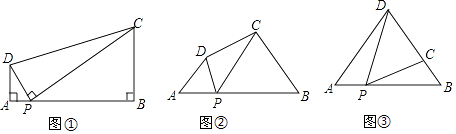
(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:ADBC=APBP.
(2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
参考答案:
【答案】
(1)证明:∵∠DPA+∠CPB=90°,∠DPA+∠ADP=90°,
∴∠PDA=∠CPB,
又∵∠A=∠B=90°,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(2)解:结论:ADBC=APBP仍然成立,
理由:∵∠ADP+∠APD=180°﹣θ,∠DPA+∠CPB=180°﹣θ,
∴∠ADP=∠CPB,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(3)解:作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,
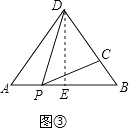
∴DE=![]() =4,
=4,
∴DC=4,
∴BC=1,
依据(1)(2)的结论AD·BC=AP·BP,
∴5×1=t(6﹣t),
∴t2﹣6t+5=0,
解得:t1=1,t2=5,
∴点P运动时间为1s或5s.
【解析】(1)由同角的余角相等得∠PDA=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]()
![]()
![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(2)结论:AD·BC=AP·BP仍然成立;理由:由等量代换得∠ADP=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(3)作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,由勾股定理得DE=DC=4,依据(1)(2)的结论AD·BC=AP·BP,即t2﹣6t+5=0,解之即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过x轴上的点M,与反比例函数y=
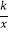 (x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.
(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.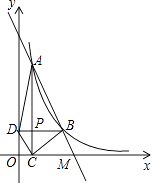
(1)求k的值;
(2)若AB=2BM,求△ABD的面积;
(3)若四边形ABCD为菱形,求直线AB的函数解析式. -
科目: 来源: 题型:
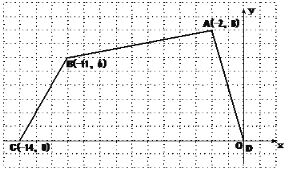
查看答案和解析>>【题目】四边形ABCD各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0)。
(1)确定这个四边形的面积,你是怎么做的?
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
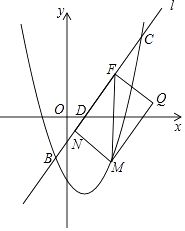
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;
(3)在(2)的条件下,已知a=﹣ ,直线l:y=
,直线l:y=  x﹣1与抛物线y=tx2﹣
x﹣1与抛物线y=tx2﹣  x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣
x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣  x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
-
科目: 来源: 题型:
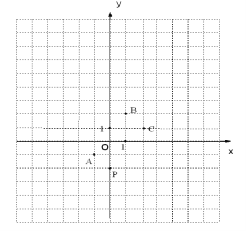
查看答案和解析>>【题目】如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,….如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:
(2)求经过第2010次跳动之后,棋子落点的位置。
相关试题

