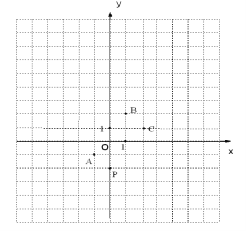
【题目】如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,….如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:
(2)求经过第2010次跳动之后,棋子落点的位置。
参考答案:
【答案】(1) M(-2,0),N(4,4);(2)(0,-2).
【解析】
(1)点P关于点A的对称点M,即是连接PA延长到M使PA=AM,所以M的坐标是M(-2,0),点M关于点B的对称点N处,即是连接PB延长到N使PB=BN,所以N的坐标是N(4,4);
(2)棋子跳动3次后又回点P处,利用这个循环的规律就可以得到棋子落点处的坐标.
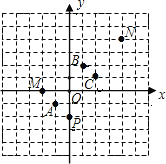
解:(1)首先发现点P的坐标是(0,-2),第一次跳到点P关于A点的对称点M处是(-2,0),跳到点M关于点B的对称点N处是(4,4);
(2)由(1)得出:则第三次再跳到点N关于点C的对称点处是(0,-2)…,发现3次一循环.又2010÷3=670,则第2010次跳动之后,棋子落点的坐标与点P坐标相同,落在了(0,-2)处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
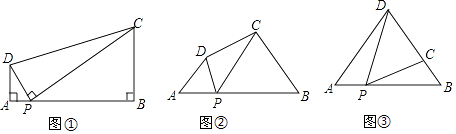
(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:ADBC=APBP.
(2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;
(3)在(2)的条件下,已知a=﹣ ,直线l:y=
,直线l:y=  x﹣1与抛物线y=tx2﹣
x﹣1与抛物线y=tx2﹣  x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣
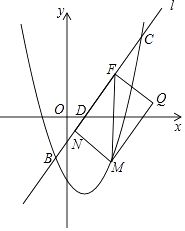
x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣  x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
-
科目: 来源: 题型:
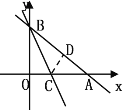
查看答案和解析>>【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各等式中成立的是( )
A.﹣ =﹣2
=﹣2
B.﹣ =﹣0.6
=﹣0.6
C.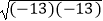 =﹣13
=﹣13
D. =±6
=±6
相关试题

