【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.

(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
参考答案:
【答案】(1)、证明过程见解析;(2)、正方形,理由见解析.
【解析】试题分析:(1)、根据CF∥AB可得∠CFE=∠DAE,∠FCE=∠ADE,根据E为中点可得CE=DE,则△ECF和△DEA全等,从而得出答案;(2)、根据AD=BD,则CF=BD,CF∥BD得出平行四边形,根据CD为AB边上的中线,CA=CB得出∠BDC=90°得出矩形,根据CD为等腰直角△ABC斜边上的中线得出CD=BD,即得到正方形.
试题解析:(1)、∵CF∥AB,∴∠CFE=∠DAE,∠FCE=∠ADE,∵E为CD的中点,∴CE=DE,
∴△ECF≌△DEA(AAS), ∴CF=AD,
(2)四边形CDBF为正方形,理由为:
∵AD=BD, ∴CF=BD; ∵CF=BD,CF∥BD,∴四边形CDBF为平行四边形,
∵CA=CB,CD为AB边上的中线,∴CD⊥AB,即∠BDC=90°,∴四边形CDBF为矩形,
∵等腰直角△ABC中,CD为斜边上的中线,∴CD=![]() AB,即CD=BD,则四边形CDBF为正方形.
AB,即CD=BD,则四边形CDBF为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
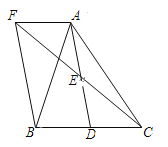
(1)求证D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:

(1)两人相遇之前,小刚的速度是 米/分,小强的速度是 米/分;
(2)求两人比赛过程中y与x之间的函数关系式;
(3)若比赛开始10分钟后,小强按原路以比赛时的速度返回,则再经过多少分钟两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的解析表达式为
的解析表达式为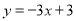 ,且
,且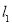 与
与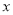 轴交于点
轴交于点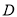 ,直线
,直线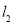 经过点
经过点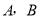 ,直线
,直线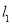 ,
, 交于点
交于点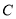 .
.(1)求点
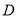 的坐标;(2)求直线
的坐标;(2)求直线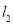 的解析表达式;(3)求
的解析表达式;(3)求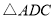 的面积;(4)在直线
的面积;(4)在直线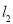 上存在异于点
上存在异于点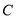 的另一点
的另一点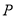 ,使得
,使得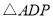 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.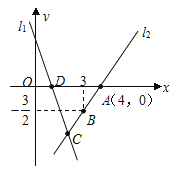
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写下列空格,完成证明.
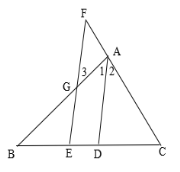
已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF∥AD,EF交AB于点G.
求证:∠3=∠F
证明:因为AD是△ABC的角平分线 ( 已知 )
所以∠1=∠2 ( )
因为EF∥AD(已知)
所以∠3=∠ ( )
∠F=∠ ( )
所以∠3=∠F( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加快推进教育现代化,某中学计划分批购买部分A品牌电脑和B品牌课桌.下表是前两次购买的情况:
A品牌电脑的数量
(单位:台)
B品牌课桌的数量
(单位:张)
总价
(单位:元)
第一次
10
200
70000
第二次
15
100
75000
(1)每台A品牌电脑和每张B品牌课桌的价格各是多少元?
(2)在“五·一”黄金周期间,经销商对一次性购买量大的客户打折优惠:一次性购买A品牌电脑不少于50台,按9折优惠;一次性购买B品牌课桌不少于450张,按8折优惠.如果学校再次购买A品牌电脑和B品牌课桌若干,恰好花去24万元,并且均享受了优惠,那么学校可能有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台)
售价(元/台)
电饭煲
200
250
电压锅
160
200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的
 ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
相关试题

