【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
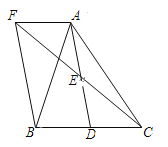
(1)求证D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
参考答案:
【答案】(1)、证明过程见解析;(2)、矩形;证明过程见解析.
【解析】
试题分析:(1)、根据AF∥BD得出∠AFE=∠DCE,根据E是中点得出AE=DE,结合∠AEF=∠DEC得出△AEF和△EDC全等,从而得出DC=AF,根据AF=BD得出BD=DC,即中点;(2)、根据AF=BD以及AF∥BD得出四边形为平行四边形,根据AB=AC,D为BC的中点得出AD⊥BC,从而说明矩形.
试题解析:(1)、∵AF∥BD,∴∠AFE=∠DCE. ∵E是AD的中点,∴AE=DE.
又∵∠AEF=∠DEC,∴△AEF≌△DEC(AAS).∴DC=AF. 又∵AF=BD,∴BD=DC. ∴D是BC的中点
(2)、四边形AFBD是矩形.
∵AF=BD,AF∥BD, ∴四边形AFBD是平行四边形. ∵AB=AC,D是BC的中点,
∴AD⊥BC,∴∠ADB=90°. ∴四边形AFBD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A.(7,1) B.B(1,7) C.(1,1) D.(2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数
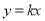 的图象与反比例函数
的图象与反比例函数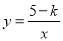 (
( 为常数,
为常数, )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.(1)求两个函数图象的交点坐标;
(2)若点
 ,
, 是反比例函数
是反比例函数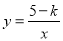 图象上的两点,且
图象上的两点,且 ,试比较
,试比较 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数
 的图象经过点C,一次函数y=ax+b的图象经过点A、C
的图象经过点C,一次函数y=ax+b的图象经过点A、C(1)求反比例函数和一次函数的解析式
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,请直接写出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:

(1)两人相遇之前,小刚的速度是 米/分,小强的速度是 米/分;
(2)求两人比赛过程中y与x之间的函数关系式;
(3)若比赛开始10分钟后,小强按原路以比赛时的速度返回,则再经过多少分钟两人相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的解析表达式为
的解析表达式为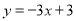 ,且
,且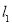 与
与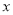 轴交于点
轴交于点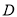 ,直线
,直线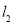 经过点
经过点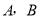 ,直线
,直线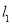 ,
, 交于点
交于点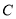 .
.(1)求点
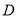 的坐标;(2)求直线
的坐标;(2)求直线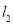 的解析表达式;(3)求
的解析表达式;(3)求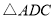 的面积;(4)在直线
的面积;(4)在直线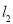 上存在异于点
上存在异于点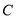 的另一点
的另一点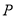 ,使得
,使得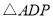 与
与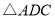 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.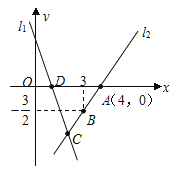
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.

(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
相关试题

