【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.

参考答案:
【答案】(1)证明见解析;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.
【解析】
试题分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;
(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.
试题解析:(1)∵AC为直径,
∴∠ADC=90°,
∴∠A+∠DCA=90°,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
解:连接DO,

∵DO=CO,
∴∠1=∠2,
∵DM=CM,
∴∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴直线DM与⊙O相切,
故当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①同位角相等; ②内错角相等 ; ③对顶角相等 ;④邻补角互补;⑤同旁内角互补
其中真命题的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a+3与2a﹣15是m的平方根,则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=3,y=1是方程3x﹣ay=2的一个解,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=
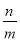 .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)=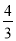 .则在以下结论:①F(5)=5;②F(24)=
.则在以下结论:①F(5)=5;②F(24)=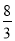 ;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有_____(填序号)
;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有_____(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程3x2﹣3x=x+2化为一般形式ax2+bx+c=0后,a、b、c的值分别是( )
A. 3、﹣4、﹣2 B. 3、﹣3、2 C. 3、﹣2、2 D. 3、﹣4、2
相关试题

