【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=
的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 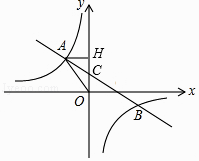
(1)求△AHO的周长;
(2)求反比例函数和一次函数的解析式.
参考答案:
【答案】
(1)解:∵AH⊥y轴于点H,
∴∠AHO=90°,
∴tan∠AOH= ![]() ,AH=4,
,AH=4,
∴OH=3,
∴由勾股定理可求出OA=5,
∴△AHO的周长为3+4+5=12
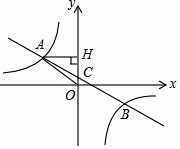
(2)解:由(1)可知:点A的坐标为(﹣4,3),
把(﹣4,3)代入y= ![]() ,可得k=﹣12,
,可得k=﹣12,
∴反比例函数的解析式为:y=﹣ ![]() ,
,
∵把B(m,﹣2)代入反比例函数y=﹣ ![]() 中,可得m=6,
中,可得m=6,
∴点B的坐标为(6,﹣2),
将A(﹣4,3)和B(6,﹣2)代入y=ax+b,可得
![]() ,
,
解得:  ,
,
∴一次函数的解析式为:y=﹣ ![]() x+1
x+1
【解析】(1)根据tan∠AOH= ![]() 求出AH的长度,由勾股定理可求出OH的长度即可求出△AHO的周长.(2)根据点A的坐标为(﹣4,3),点A在反比例函数的图象上,可求出k的值,将点B的坐标代入反比例函数的解析式中求出m的值,然后将A、B两点的坐标代入一次函数解析式中即可求出该一次函数的解析式.
求出AH的长度,由勾股定理可求出OH的长度即可求出△AHO的周长.(2)根据点A的坐标为(﹣4,3),点A在反比例函数的图象上,可求出k的值,将点B的坐标代入反比例函数的解析式中求出m的值,然后将A、B两点的坐标代入一次函数解析式中即可求出该一次函数的解析式.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和解直角三角形的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,添加下列条件,还不能使△ABC≌△CDA成立的是( )

A. AD=BC B. ∠BAC=∠ACD C. AB∥DC D. AB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAD的度数为( )
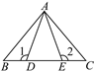
A. 50° B. 60° C. 70° D. 110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为
 .
.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由.
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为
 ”,那么满足这一条件,且彼此不全等的三角形共有 个.
”,那么满足这一条件,且彼此不全等的三角形共有 个.友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
-
科目: 来源: 题型:
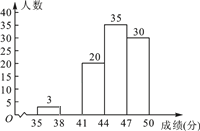
查看答案和解析>>【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分)
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
人数
1
2
3
3
6
7
5
8
15
9
11
12
8
6
4
成绩分组
频数
频率(百分比)
35≤x<38
3
0.03
38≤x<41
a
0.12
41≤x<44
20
0.20
44≤x<47
35
0.35
47≤x≤50
30
b
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
相关试题

