【题目】![]() 、
、![]() 两地相距
两地相距![]() 千米,一列慢车从
千米,一列慢车从![]() 地开出,每小时行驶
地开出,每小时行驶![]() 千米,一列快车从
千米,一列快车从![]() 地开出,每小时行驶
地开出,每小时行驶![]() 千米,两车同时开出.
千米,两车同时开出.
![]() 若相向而行,出发后多少小时相遇?
若相向而行,出发后多少小时相遇?
![]() 若相背而行,多少小时后,两车相距
若相背而行,多少小时后,两车相距![]() 千米
千米
![]() 若两车同向而行,快车在慢车后面,多少小时后,快车追上慢车?
若两车同向而行,快车在慢车后面,多少小时后,快车追上慢车?
参考答案:
【答案】(1)若相向而行,出发后![]() 小时相遇;(2)若两车同向而行,快车在慢车后面,
小时相遇;(2)若两车同向而行,快车在慢车后面,![]() 小时后,快车追上慢车.
小时后,快车追上慢车.
【解析】
(1)设出发后x小时两车相遇,根据两地间距=相遇时间×两车速度之和,即可列出关于x的一元一次方程,解方程即可;
(2)设y小时后两车相距800千米,根据行驶时间×两车速度和=两车间距-两地间距,即可列出关于y的一元一次方程,解方程即可;
(3)设出发后z小时快车追上慢车,根据两地间距=相遇时间×两车速度之差,即可列出关于z的一元一次方程,解方程即可.
(1)设出发后x小时相遇,
根据题意,可得(80+120)x=600,
解得x=3.
答:若相向而行,出发后3小时相遇;
(2)设y小时后两车相距800千米,
根据题意,可得(80+120)y=800-600,
解得y=1.
答:若相背而行,1小时后,两车相距800千米;
(3)设z小时后快车追上慢车,
根据题意,可得(120-80)z=600,
解得z=15.
答:若两车同向而行,快车在慢车后面,15小时后,快车追上慢车.
-
科目: 来源: 题型:
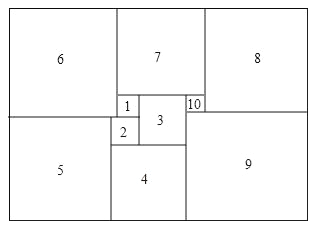
查看答案和解析>>【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算:
(1)如果标注1、2的正方形边长分别为1,2,第3个正方形的边长= ;第5个正方形的边长= ;
(2)如果标注1、2的正方形边长分别为x,y,第10个正方形的边长= .(用含x、y的代数式表示)
-
科目: 来源: 题型:
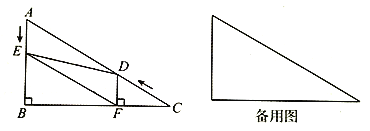
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.×
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式组
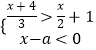 .
.
(1)当a=3时,解这个不等式组;
(2)若不等式组的解集是x<1,求a的值. -
科目: 来源: 题型:
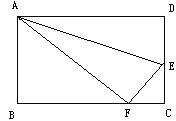
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,点D落在BC边的点F处, 已知BC=10厘米,AB=8厘米,求FC和EF的长.
相关试题

