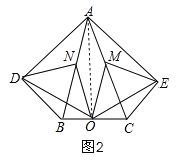
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

参考答案:
【答案】(1)证明见解析(2)当∠DAB等于35°时,四边形ADOE是菱形
【解析】试题分析:(1)根据直角三角形斜边中线等于斜边一半得:DN=![]() AB,由中位线定理得:OM=
AB,由中位线定理得:OM=![]() AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
(2)连接AO,当∠DAB等于35°时,四边形ADOE是菱形,如图2,设∠DAB=x°,则∠BND=2x°,易证得OD=OE,AD=AE,因此只要AD=OD,四边形ADOE就是菱形;即∠DAO=∠AOD,列关于x的方程解出即可.
试题解析:证明:(1)∵∠ADB=90°,N是AB的中点,∴DN=![]() AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=
AB=AN,∴∠ADN=∠BAD,∵O是AB的中点,M是AC的中点,∴OM是△ABC的中位线,∴OM=![]() AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=
AB,OM∥AB,∴∠OMC=∠BAC,同理得:∠BNO=∠BAC,∴∠BNO=∠OMC,∵DN=![]() AB,OM=
AB,OM=![]() AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
AB,∴DN=OM,同理得:ME=ON,∵∠BND=∠ADN+∠BAD,∠CME=∠CAE+∠AEM,∴∠BND=2∠BAD,∠CME=2∠CAE,∵∠BAD=∠CAE,∴∠BND=∠CME,∴∠BND+∠BNO=∠CME+∠OMC,即∠DNO=∠EMO,∴△EMO≌△OND;
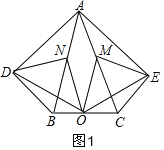
(2)当∠DAB等于35°时,四边形ADOE是菱形,理由是:
如图2,连接AO,设∠DAB=x°,则∠BND=2x°,∵AB=AC,O是BC的中点,∴AO平分∠BAC,AO⊥BC,∵∠BAC=40°,∴∠BAO=20°,在Rt△ABO中,N是AB的中点,∴ON=![]() AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=
AB=AN,∴∠BAO=∠AON=20°,∴∠BNO=40°,由(1)得:ON=![]() AC,DN=
AC,DN=![]() AB,∴ON=DN,∴∠NDO=∠NOD=
AB,∴ON=DN,∴∠NDO=∠NOD=![]() (180°-∠DNO)=90°﹣
(180°-∠DNO)=90°﹣![]() (2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
(2x°+40°)=70°﹣x°,∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,∴△ADB≌△AEC,∴AD=AE,由(1)得:△EMO≌△OND,∴OD=OE,∴当AD=OD时,四边形ADOE是菱形,即∠DAO=∠AOD,x+20=70﹣x+20,x=35,∴当∠DAB等于35°时,四边形ADOE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,点F在AC延长线上,
 ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
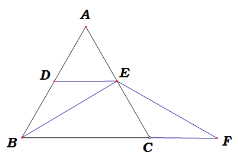

图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A的坐标是(a,0),点B的坐标是(b,0),其中a,b满足
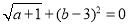 .
.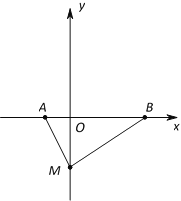
(1)填空:a=______,b=_______;
(2)在
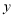 轴负半轴上有一点M(0,m),三角形ABM的面积为4.
轴负半轴上有一点M(0,m),三角形ABM的面积为4.①求m的值;
②将线段AM沿x轴正方向平移,使得A的对应点为B,M的对应点为N. 若点P为线段AB上的任意一点(不与A,B重合),试写出∠MPN,∠PMA,∠PNB之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和2件B商品,可获得利润45元;销售8件A商品和4件B商品,可获得利润80元.
(1)求A、B两种商品的销售单价;
(2)如果该商场计划购进A、B两种商品共80件,用于进货资金最多投入2 000元,但又要确保获利至少590元,请问有那几种进货方案?
相关试题

