搜索
【题目】二次函数y=ax2+bx+c的图像如图所示，则反比例函数 
与一次函数y=bx+c在同一坐标系中的大致图像是（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】解：∵二次函数的图像开口向下，
∴反比例函数y= 
的图像必在二、四象限，故A、C错误；
∵二次函数的图像经过原点，
∴c=0，
∴一次函数y=bx+c的图像必经过原点，故B错误．
故选D．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
-
科目： 来源： 题型：
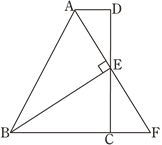
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F. 已知AD=2cm，BC=5cm.
（1）求证：FC=AD；
（2）求AB的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学课上，李老师出示了如下框中的题目．
在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图．试确定线段AE与DB的大小关系，并说明理由．
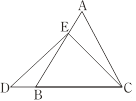
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：
AE DB(填“＞”，“＜”或“＝”)．
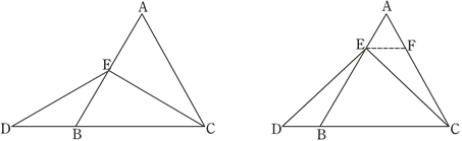
图1 图2
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE DB(填“＞”，“＜”或“＝”)．
理由如下：如图2，过点E作EF∥BC，交AC于点F.
(请你完成以下解答过程)
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长(请你直接写出结果)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空：
如图所示，已知∠1 = ∠2，∠B = ∠C，可推得AB∥CD，
理由如下：
∵∠1 = ∠2（已知），且∠1 = ∠4（_____________________），
∴∠2 = ∠4（等量代换）.
∴CE∥BF（__________________________）.
∴∠_____= ∠3（________________________）
又∵∠B = ∠C（已知），
∴∠3= ∠B（等量代换），
∴AB∥CD（_____________________________）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知下面四个图形中，AB∥CD，探究四个图形中，∠APC与∠PAB，∠PCD的数量关系.
（1）图①中，∠APC与∠PAB，∠PCD的关系是__________________；
（2）图②中，∠APC与∠PAB，∠PCD的关系是__________________；
（3）请你在图③和图④中任选一个，说明∠APC与∠PAB，∠PCD的关系，并加以证明
-
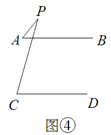
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=3x2﹣6x+k（k为常数）的图像经过点A（0.8，y1），B（1.1，y2），C（
，y3），则有（ ）
A.y1＜y2＜y3
B.y1＞y2＞y3
C.y3＞y1＞y2
D.y1＞y3＞y2 -
科目： 来源： 题型：
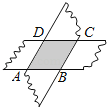
查看答案和解析>>【题目】如图，剪两张对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是 ．
相关试题
