【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
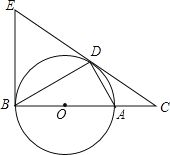
(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见解析;(2)5
【解析】
试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() ,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
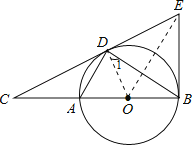
(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
∴![]()
![]() ,
,
∴CD=![]() ×12=8,
×12=8,
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,
解得x=5.
即BE的长为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x﹣10=90 B.0.08x﹣10=90 C.90﹣0.8x=10 D.x﹣0.8x﹣10=90
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
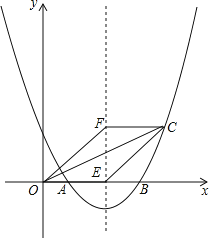
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则下列各式中不成立的是( )
A.a+2<b+2
B.﹣3a<﹣3b
C.2﹣a>2﹣b
D.3a<3b -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=(m﹣1)x2+2x+1的图象与x轴有两个不同的交点,则m的取值范围是( )
A. m≤2 B. m<2 C. m≤2且m≠1 D. m<2且m≠1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式的括号内填上恰当的项,x2﹣y2+8y﹣4=x2﹣(___________).
相关试题

