【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
参考答案:
【答案】(1)4种,甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50(2)甲47,乙53利润最大,最大利润1106元
【解析】
(1)利用购书款不高于1118元,预计这100本图书全部售完的利润不低于1100元,结合表格中数据得出不等式组,求出即可;
(2)设利润为W,根据题意得W=10x+12(100-x)=-2x+1200,W随x的增大而减小,故购进甲种书:47种,乙种书:53本利润最大,代入求出即可;
解:(1)设购进甲种图书x本,则购进乙书(100-x)本,根据题意得出:
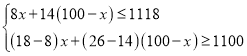
解得:47≤x≤50.
故有4种购书方案:甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50;
(2)设利润为W,根据题意得
W=10x+12(100-x)=-2x+1200,
根据一次函数的性质得,W随x的增大而减小,
故购进甲种书:47本,乙种书:53本,利润最大,
最大利润W=-2×47+1200=1106,
所以甲47,乙53利润最大,最大利润1106元.
故答案为:(1)4种,甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50(2)甲47,乙53利润最大,最大利润1106元
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了依次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
各组人数统计表
组号
年龄分组
频数(人)
频率
第一组
20≤x<25
50
0.05
第二组
25≤x<30
a
0.35
第三组
35≤x<35
300
0.3
第四组
35≤x<40
200
b
第五组
40≤x≤45
100
0.1
(1)求本次调查的样本容量及表中的a、b的值;
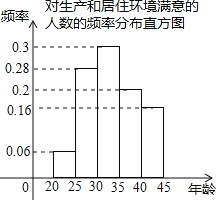
(2)调查结果得到对生产和居住环境满意的人数的频率分布直方图如图,政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
(3)从第二张和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,y=x的图象向右平移1个单位得到y=x﹣1的图象,类似的,y=
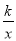 (k≠0)的图象向左平移2个单位得到y=
(k≠0)的图象向左平移2个单位得到y=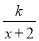 (k≠0)的图象.请运用这一知识解决问题.
(k≠0)的图象.请运用这一知识解决问题.如图,已知反比例函数y=
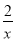 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(1,m)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(1,m)和点B.(1)写出点B的坐标,并求a的值;
(2)将函数y=
 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C1和l1,已知图象C1经过点M(3,2).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C1和l1,已知图象C1经过点M(3,2).①分别写出平移后的两个图象C1和l1对应的函数关系式;
②直接写出不等式
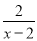 +4≤ax的解集.
+4≤ax的解集.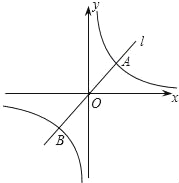
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】货轮上卸下若干只箱子,其总重量为10t,每只箱子的重量不超过1t,为保证能把这些箱子一次运走,问至少需要多少辆载重3t的汽车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
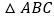 中,
中,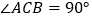 ,
,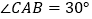 ,
,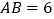 ,以线段
,以线段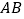 为边向外作等边
为边向外作等边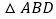 ,点
,点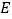 是线段
是线段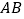 的中点,连结
的中点,连结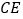 并延长交线段
并延长交线段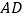 于点
于点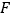 .
.(1)求证:四边形
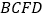 为平行四边形;
为平行四边形;(2)求平行四边形
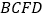 的面积;
的面积;(3)如图,分别作射线
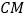 ,
,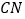 ,如图中
,如图中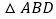 的两个顶点
的两个顶点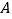 ,
,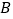 分别在射线
分别在射线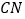 ,
,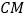 上滑动,在这个变化的过程中,求出线段
上滑动,在这个变化的过程中,求出线段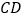 的最大长度.
的最大长度.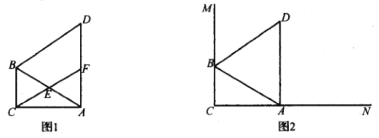
-
科目: 来源: 题型:
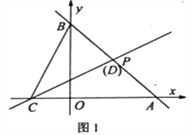
查看答案和解析>>【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:
 交线段AB于点D。
交线段AB于点D。如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若
 ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。

相关试题

