【题目】货轮上卸下若干只箱子,其总重量为10t,每只箱子的重量不超过1t,为保证能把这些箱子一次运走,问至少需要多少辆载重3t的汽车?
参考答案:
【答案】需5辆汽车.
【解析】试题分析:易得每次运走的质量应在2t和3t之间,可表示出n辆车可运走的总质量的关系式,求得一次运走的整数解,进而判断假如有13只箱子的时候需要汽车的辆数即可.
试题解析:设共需n辆汽车,它们运走的重量依次为a1,a2,an则
2≤ai≤3(i=1,2,…,n),al+a2+…+an=10
∴2n≤10≤3n,解得![]() .
.
∵车子数n应为整数,∴n=4或5,但4辆车子不够.
例如有13只箱子,每只重量为![]() ,而3×
,而3×![]() <3,4×
<3,4×![]() >3,即每辆车子只能运走3只箱子,4辆车子只能运走12只箱子,还剩一只箱子,故需5辆汽车.
>3,即每辆车子只能运走3只箱子,4辆车子只能运走12只箱子,还剩一只箱子,故需5辆汽车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,y=x的图象向右平移1个单位得到y=x﹣1的图象,类似的,y=
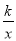 (k≠0)的图象向左平移2个单位得到y=
(k≠0)的图象向左平移2个单位得到y=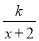 (k≠0)的图象.请运用这一知识解决问题.
(k≠0)的图象.请运用这一知识解决问题.如图,已知反比例函数y=
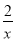 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(1,m)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(1,m)和点B.(1)写出点B的坐标,并求a的值;
(2)将函数y=
 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C1和l1,已知图象C1经过点M(3,2).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C1和l1,已知图象C1经过点M(3,2).①分别写出平移后的两个图象C1和l1对应的函数关系式;
②直接写出不等式
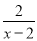 +4≤ax的解集.
+4≤ax的解集.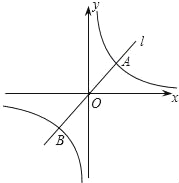
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书
乙种图书
进价(元/本)
8
14
售价(元/本)
18
26
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
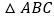 中,
中,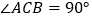 ,
,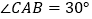 ,
,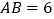 ,以线段
,以线段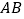 为边向外作等边
为边向外作等边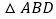 ,点
,点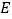 是线段
是线段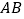 的中点,连结
的中点,连结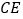 并延长交线段
并延长交线段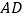 于点
于点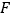 .
.(1)求证:四边形
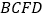 为平行四边形;
为平行四边形;(2)求平行四边形
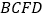 的面积;
的面积;(3)如图,分别作射线
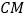 ,
,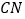 ,如图中
,如图中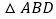 的两个顶点
的两个顶点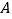 ,
,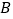 分别在射线
分别在射线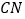 ,
,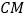 上滑动,在这个变化的过程中,求出线段
上滑动,在这个变化的过程中,求出线段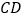 的最大长度.
的最大长度.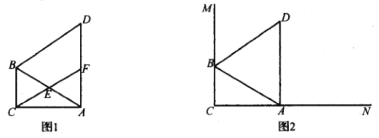
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:
 交线段AB于点D。
交线段AB于点D。如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若
 ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。
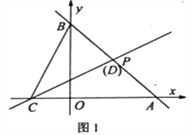

-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2B. x2-62=(10-x)2
C. x2+62=(10-x)2D. x2+6=(10-x)2
相关试题

