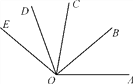
【题目】如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
参考答案:
【答案】40°.
【解析】试题分析:(1)根据角平分线的定义可以求得∠BOD=∠AOB+∠DOE;
(2)根据角平分线的定义易求得∠EOC=2∠COD=60°,所以由图中的角与角间的和差关系可以求得∠AOC=80°,最后由角平分线的定义求解.
试题解析:解:(1)因为OB为∠AOC的平分线,OD是∠COE的平分线,
所以∠AOB=∠BOC,∠DOE=∠DOC.
所以∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°.
(2)因为OD是∠COE的平分线,∠COD=30°,
所以∠EOC=2∠COD=60°.
因为∠AOE=140°,∠AOC=∠AOE-∠EOC=80°.
又因为OB为∠AOC的平分线,
所以∠AOB=![]() ∠AOC=40°.
∠AOC=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。(1)求抛物线的解析式;
(2)如图1若R为y轴上的一个动点,连接AR,则

 RB+AR的最小值为
RB+AR的最小值为 (3)在x轴上取一动点P(m,0),
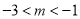 ,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.(4)设此抛物线的对称轴为直线MN,在直线MN上取一点T,使∠BTN=∠CTN.直接写出点T的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2+y2)2-2(x2+y2)-3=0,则x2+y2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).

-
科目: 来源: 题型:
查看答案和解析>>【题目】把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式2x2﹣3x+5是次项式.
相关试题

