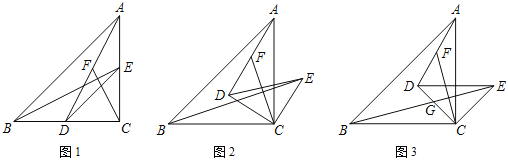
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别为AC,BC上的点,且CE=CD,连接DE,AD,BE,F为线段AD的中点,连接CF.
(1)求证:BE=2CF;
(2)如图2,把△DEC绕点C顺时针旋转α角(0°<α<90°),其他条件不变,试探究线段BE与CF的位置关系,并说明理由;
(3)如图3,把△DEC绕点C顺时针旋转45°,BE,CD交于点G.若∠DCF=30°,求![]() 及
及![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;
(2)BE⊥CF.证明见解析;
(3)![]() ,
, ![]()
【解析】试题分析:(1)根据已知条件易证△BCE≌△ACD,即可得BE=AD,∠EBC=∠DAC,再由F为线段AD的中点可得CF=AF=DF=![]() AD,即可证得结论;(2)延长CF到H,使HF=CF,连接AH、DH,易得四边形AHDC为平行四边形,根据平行四边形的性质可得AH=CD=CE,∠CAH=180°-∠ACD,再由∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,即可得∠CAH=∠BCE,再判定△CAH≌△BCE,根据全等三角形的性质可得∠ACH=∠CBE,所以∠CBE+∠BCH=∠ACH+∠BCH=90°,即可得结论BE⊥CF ;( 3)设BE,CF相交于点O,则∠GOC=90°,作BC的垂直平分线,交BG于点M,连接CM则BM=CM,∠MBC=∠MCB,所以∠OMC=2∠MBC,再求得∠DCA=45°,∠OMC=30°,设OG=x,则CG=2x,OC=
AD,即可证得结论;(2)延长CF到H,使HF=CF,连接AH、DH,易得四边形AHDC为平行四边形,根据平行四边形的性质可得AH=CD=CE,∠CAH=180°-∠ACD,再由∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,即可得∠CAH=∠BCE,再判定△CAH≌△BCE,根据全等三角形的性质可得∠ACH=∠CBE,所以∠CBE+∠BCH=∠ACH+∠BCH=90°,即可得结论BE⊥CF ;( 3)设BE,CF相交于点O,则∠GOC=90°,作BC的垂直平分线,交BG于点M,连接CM则BM=CM,∠MBC=∠MCB,所以∠OMC=2∠MBC,再求得∠DCA=45°,∠OMC=30°,设OG=x,则CG=2x,OC=![]() x,BM=CM=2
x,BM=CM=2![]() x,OM=
x,OM=![]() OC=3x,MG=3x-x=2x,求得BG=BM+MG=2
OC=3x,MG=3x-x=2x,求得BG=BM+MG=2![]() x+2x,BO=BM+MO=2
x+2x,BO=BM+MO=2![]() x+3x,即可得
x+3x,即可得![]() ,
, ![]() ,过E作BC的垂线,交BC的延长线于N,则Rt△BNE∽Rt△BOC,可得
,过E作BC的垂线,交BC的延长线于N,则Rt△BNE∽Rt△BOC,可得![]() ,设EN=t,则CN=
,设EN=t,则CN=![]() t,CE=t,BN=(
t,CE=t,BN=(![]() +2)t,BC=(
+2)t,BC=(![]() +2)t-t=(
+2)t-t=(![]() +1)t,求得
+1)t,求得![]() 的值,又因AB=BC,CD=CE,即可求得
的值,又因AB=BC,CD=CE,即可求得![]() 的值.
的值.
试题解析:
(1)证明:∵AC=BC,DC=EC,∠ACB=90°
∴△BCE≌△ACD
∴BE=AD,∠EBC=∠DAC
∵F为线段AD的中点
∴CF=AF=DF= ![]() AD
AD
∴BE=2CF
(2)BE⊥CF.证明如下:
证明:如图2,延长CF到H,使HF=CF,连接AH、DH
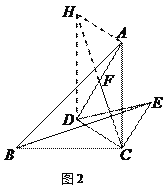
∵AF=DF,∴四边形AHDC为平行四边形
∴AH=CD=CE,∠CAH=180°-∠ACD
∵∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD
∴∠CAH=∠BCE
又∵AC=BC,∴△CAH≌△BCE
∴∠ACH=∠CBE
∴∠CBE+∠BCH=∠ACH+∠BCH=90°
∴BE⊥CF
(3)如图3,设BE,CF相交于点O,
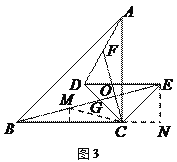
则∠GOC=90°
作BC的垂直平分线,交BG于点M,连接CM
则BM=CM,∠MBC=∠MCB
∴∠OMC=2∠MBC
∵AC⊥DE,∠CDE=45°,∴∠DCA=45°
∵∠DCF=30°
∴∠ACO=∠CBE=15°,∴∠OMC=30°
设OG=x,则CG=2x,OC=![]() x,BM=CM=2
x,BM=CM=2![]() x
x
OM=![]() OC=3x,MG=3x-x=2x
OC=3x,MG=3x-x=2x
∴BG=BM+MG=2![]() x+2x,BO=BM+MO=2
x+2x,BO=BM+MO=2![]() x+3x
x+3x
∴![]() =
= ![]() =
=![]() +1
+1
![]() =
= ![]() =
=![]() +2
+2
过E作BC的垂线,交BC的延长线于N
则Rt△BNE∽Rt△BOC,∴![]() =
= ![]() =
=![]() +2
+2
设EN=t,则CN=t,CE=![]() t,BN=(
t,BN=(![]() +2)t,BC=(
+2)t,BC=(![]() +2)t-t=(
+2)t-t=(![]() +1)t
+1)t
∴![]() =
= ![]() =
= ![]()
∵AB=BC,CD=CE,∴ ![]() =
= ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2+3x﹣40=0.
-
科目: 来源: 题型:
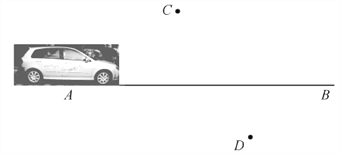
查看答案和解析>>【题目】如图所示,一辆汽车在直线形的公路AB上由A向B行驶,C,D分别是位于公路AB两侧的村庄.
(1)该汽车行驶到公路AB上的某一位置C′时距离村庄C最近,行驶到D′位置时,距离村庄D最近,请在公路AB上作出C′,D′的位置(保留作图痕迹);
(2)当汽车从A出发向B行驶时,在哪一段路上距离村庄C越来越远,而离村庄D越来越近?(只叙述结论,不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】当|a|=﹣a时,则a是( )
A. a≤0B. a<0C. a≥0D. a>0
-
科目: 来源: 题型:
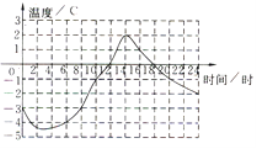
查看答案和解析>>【题目】如图所示的图象记录了某地一月份某天的温度随时间变化.的情况,请你仔细观察图象回答下面的问题:
(1)20时的温度是 ℃,温度是0℃时的时刻是 时,最暖和的时刻是 时,温度在-3℃以下的持续时间为 时;
(2)从图象中还能获取哪些信息?(写出1~2条即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.菱形都是相似图形B.矩形都是相似图形
C.等边三角形都是相似图形D.各边对应成比例的多边形是相似多边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= BD;
BD;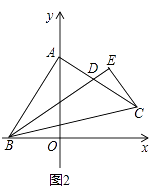
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.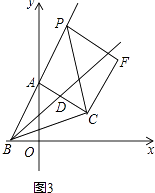
相关试题

