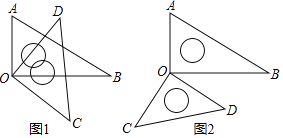
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图1,若∠BOD=25°,则∠AOC= °;若∠AOC=125°,则∠BOD= °;
(2)如图2,若∠BOD=50°,则∠AOC= °;若∠AOC=140°,则∠BOD= °;
(3)猜想∠AOC与∠BOD的大小关系: ;并结合图(1)说明理由.
参考答案:
【答案】(1)155,55;(2)130,40;(3)∠AOC与∠BOD互补,理由见解析.
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD﹣∠BOD可分别计算出∠AOC、∠BOD的度数;
(2)根据∠AOC=∠AOB+∠COD﹣∠BOD计算可得;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180![]() 且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
解:(1)若∠BOD=25![]() ,
,
∵∠AOB=∠COD=90![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣25
﹣25![]() =155
=155![]() ,
,
若∠AOC=125![]() ,
,
则∠BOD=∠AOB+∠COD﹣∠AOC=90![]() +90
+90![]() ﹣125
﹣125![]() =55
=55![]() ;
;
故答案为:155,55.
(2)若∠BOD=50![]() ,
,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90![]() +90
+90![]() ﹣50
﹣50![]() =130
=130![]() ,
,
若∠AOC=140![]() ,
,
则∠BOD=360![]() ﹣∠AOC﹣∠AOB﹣∠COD=40
﹣∠AOC﹣∠AOB﹣∠COD=40![]() ;
;
故答案为:130,40.
(3)∠AOC与∠BOD互补.
∵∠AOD+∠BOD+∠BOD+∠BOC=180![]() ,∠AOD+∠BOD+∠BOC=∠AOC,
,∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180![]() ,
,
即∠AOC与∠BOD互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的抛物线是二次函数
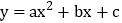 (a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有
(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有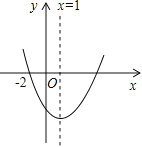
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记
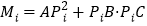 (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )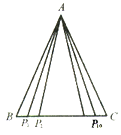
A. 4 B. 14 C. 40 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在
 中,
中, ,
,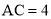 ,
,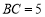 ,
,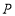 为边
为边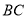 上一个动点,
上一个动点,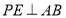 于点
于点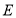 ,
,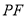 上
上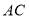 于点
于点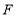 ,
,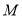 为
为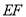 的中点,则
的中点,则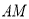 的最小值是( )
的最小值是( )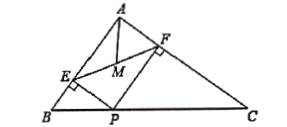
A.
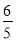 B.
B.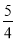
C.
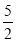 D.
D.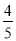
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )

A.∠A=∠1+∠2B.2∠A=∠1+∠2
C.3A=∠1+∠2D.3∠A=2(∠1+∠2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形
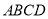 中,
中,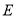 、
、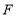 是对角线
是对角线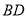 上不同的两点,下列条件中,不能得到四边形
上不同的两点,下列条件中,不能得到四边形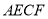 一定为平行四边形的是( )
一定为平行四边形的是( )A.
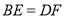 B.
B.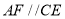 C.
C.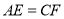 D.
D.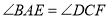
相关试题

